I det här blogginlägget skall vi kika närmare på det som kallas för primtal. Vi skall undersöka hur man egentligen kan hitta hitta dessa tal, vad de används till och om man kan få bra betalt för att hitta dem?

Vad ett primtal är och vad de är bra för

Ett primtal är ett tal som endast är delbart med 1 och sig själv. Vad betyder egentligen detta? Jo för att ett tal p skall vara ett primtal så kan det inte finnas något tal mellan 1 och p som delar just det tal (så att ett helta ges som resultat).

Exempel på primtal kan vara 7, 23 eller 29. Inget av dessa tal kan delas med något annat än sig själv eller 1. Exempel på tal som inte är primtal kan vara 9, 15, 21. Alla dessa tal är exempelvis delbara med talet 3.

Så vad används egentligen primtal till? Idag är det framförallt inom datorsäkerhet som dessa primtal används inom det som kallas för RSA kryptering. Dessa tal och produkter av dessa har visat sig vara mycket användbara för att säkert kunna skicka information mellan datorer.

Hur hittar du primtal på ett effektivt sätt?

Matematiker har genom alla tider varit väldigt intresserade av primtal och letat efter de allra bästa algoritmerna för att hitta just primtal. I vissa fall så har även detta visat sig vara lönsamt (se mer nedan).

I den allra enklaste formen av algoritm (instruktioner/metod för att lösa något eller hitta något) så skulle man kunna ta ett tal och sedan testa om det finns något tal mindre än detta tal som delar ursprungstalet. Det här innebär att algoritmen kommer att vara väldigt ineffektiv. Om vi letar efter mycket stora primtal så kommer vi (dvs datorn) att få jobba väldigt, väldigt mycket.

Nu finns det diverse olika algoritmer för att snabbare hitta primtal där den kändaste nog är Eratosthenes såll. Eratosthenes levde cirka 200 f.Kr. och är bland annat känd för att han kunde bestämma jordens storlek. Han gjorde alltså även en algoritm kallad för Eratosthenes såll som lyder enligt följande:

1. Gör en lista på alla tal från 2 till ett högsta tal, vi kallar det högsta talet för m.
2. Ta bort alla jämna tal från listan som är större än 2. (Ett alternativ för oss som har datorer är att direkt göra en lista på alla udda tal större än 2).
3. Det första talet i listan är nu ett primtal (talet 3 vid första iterationen).
4. Ta nu bort alla tal som är delbara av det första primtalet. Dessa tal kan ju inte vara ett primtal.
5. Upprepa nu steg 3 och 4 tills du har nått ett tal som är större än kvadratroten ur ditt maxtal m.
6. De tal som blir kvar i listan är nu primtal.

Om du sätter dig in i metoden här ovan så kommer du att märka att i jämförelse med den första, mer tidskrävande metoden, så finns det ett antal olika effektiviseringar av algoritmen. Men många matematiker anser ändå att denna metod är allt för tidskrävande och effektiv och har därför utvecklat ännu mer avancerade metoder för att hitta så stora primtal som möjligt.

Bland annat så finns det ett projekt som heter GIMPS (Great Internet Mersenne Prime Search) där man använder internets hjälp för att använda flera datorer världen över för att hitta primtal. Med hjälp av detta har de hittat det enormt stora primtalet $2^{57,885,161}-1$.

Kan man få betalt för att hitta primtal?

Ibland hör man rykten om att det faktiskt skulle kunna gå att tjäna pengar på att hitta primtal då dessa är så eftertraktade inom kryptografin. Detta stämmer dock bara med viss modifikation. Det finns visserligen priser som belönar de som hittar extremt stora primtal. Du kan exempelvis få 250 000 $ av Electronic Frontier Foundation om du hittar ett primtal med över 1,000,000,000 siffror. Det här är dock extremt svårt och kräver mängder av datorkapacitet och tur.

Men att företag som använder RSA kryptering skulle vara intresserade av stora primtal stämmer tydligen inte. Det behövs egentligen inte särskilt stora primtal för att just denna typ av kryptering skall vara säker.

Ibland kan det kännas långt borta att förstå vad matematiken man lär sig om i skolan egentligen kan användas till? Visserligen brukar de flesta i alla fall ha en känsla för att matematiken ligger till grund för fysikens lagar, beräkningar i kemi, biologi och ekonomi men det kan ändå kännas lite långt borta till de verkliga tillämpningarna.

Men det finns områden där man nästan direkt har nytta av att förstå trigonometri, geometri och många av matematikens områden i gymnasiekurserna. Ett av dessa är spelprogrammering och vad passar väl bättre då än att fråga någon som har skrivit en bok om just spelprogrammering i HTML5 och Javascript hur man egentligen kopplar ihop dessa bägge områden.

Så i det här blogginlägget intervjuar vi Mikael Tylmad, som har skrivit en bok i ämnet, om spelprogrammering och matematik.

Kan du beskriva lite kort vem du är och vad du jobbar med och brinner för?

Jag heter Mikael Tylmad, bor i Stockholm och arbetar främst som systemadministratör på en högstadieskola. På skolan arbetar jag mycket med linux och programmering, oftast programmering mot webben. Så ofta som möjligt (minst varje vecka) umgås jag med eleverna i skolans datorklubb där jag lär ut programmering, och de spelar en hel del minecraft. Men det är helt ok, eftersom de givetvis använder minecraft-moddar där man kan programmera! Ibland åker jag på uppdrag med min firma och håller föreläsningar på gymnasiet om programmering, nu senast för teknik-fyrorna på Tumba Gymnasium.

Jag brinner för att göra programmeringsundervisning roligare och mer tillgänglig. Programmering borde finnas i många ämnen, speciellt i fysik och matematik.

Du har skrivit en bok om att programmera spel i html5 och javascript, varför skall man göra spel i dessa tekniker?

Webben är den plattform som alla befinner sig i numera. Det säljs till och med datorer med enbart webbläsare och inget annat. Om man lär sig skapa spel och annat roligt med HTML5 och JavaScript, når man i princip alla användare. Det spelar ingen roll om de använder en dator, surfplatta eller telefon.

Det är dessutom väldigt roligt och enkelt att sätta igång med programmering i HTML5 och JavaScript, man når resultat snabbt!

Vad tycker du om javascript som programmeringsspråk?

JavaScript är ett programmeringsspråk som är väldigt bekvämt att använda. Det går att skriva kod som ser ”traditionell” ut, men det finns även möjligheter att skriva väldigt dynamisk och modern kod. Som nybörjare behöver man inte fördjupa sig i någon större teori, men som avancerad programmerare kan man verkligen spexa till sin kod!

Jag tycker definitivt att JavaScript passar som utbildningsspråk samtidigt som det är häftigt och modernt.

Om du skulle ge ditt bästa tips till någon som vill lära sig programmering, vilket skulle det då vara?

Ge dig själv en uppgift, exempelvis: Jag vill skapa spelet ”Masken”, och sätt sedan igång! Välj ett programmeringsspråk i början som är enkelt att använda, som exempelvis JavaScript där man bara behöver en enkel textredigerare och en webbläsare för att sätta igång.

Om man aldrig programmerat någonsin kan det kännas svårt att sätta igång. Börja då med att hitta en guide på nätet, eller i en bok (som exempelvis min) och följ den. Att programmera tillsammans med en kompis är också jättebra.

Om du fastnar så ska du Googla och hitta andra som gjort samma sak, försök reproducera deras lösningar, ändra några saker och se till att du förstår vad deras lösningar gör.

Vilken användning har du idag av dina matematikkunskaper när du programmerar?

När man programmerar hemsidor och olika webbapplikationer använder man sällan någon större mängd matematik. Men när man programmerar spel kommer matematik in lite här och där, speciellt när man vill göra spelen mer verklighetstrogna.

Jag gillar också att pyssla med ”matematiska konstverk”, exempelvis fraktaler. Då kombinerar man verkligen matematik med programmering och får fram häftiga bilder. Det kan exempelvis se ut så här:

Mandelbrotmängden (denna tar ett tag för din webbläsare att räkna ut):

Ett annat konkret exempel när jag fått nytta av matematik är när man vill skapa tredimensionella figurer som roterar och rör sig. Då behöver man linjär algebra som man oftast lär sig på högskolan, direkt efter gymnasiet (eller under gymnasiet om man är intresserad). Det kan se ut så här:

En roterande kub

Vad minns du själv från dina studier i matematik på gymnasiet? Vad tyckte du om matematik då?

Innan gymnasiet tyckte jag att matematik var rätt roligt, och under gymnasiet blev det lite tråkigare och tråkigare, och när jag sedan läste enbart matematik under en hel termin på Stockholms Universitet tyckte jag att det nog inte var något för mig egentligen, och började istället enbart plugga programmering.

Matematiken på min gymnasieskola var väldigt abstrakt och jag förstod väldigt sällan vad jag kunde använda den till, egentligen. Det är först nu under de senaste åren som jag hittat flera roliga tillämpningar på gymnasiematten och högskolematten, vilket har gjort att jag återupptäckt hur häftigt det faktiskt kan vara med matematik.

Om du skulle ge två tips till alla som pluggar matte för tillfället – vilka skulle det vara då?

Tips nummer ett: Lägg ned tid och energi på inlämningsuppgifter och försök göra resultaten så fina som möjligt. Experimentera med olika sätt att skapa svaren med din dator, använd exempelvis online-baserade grafräknare eller lär dig skriva dokument med LaTeX. Det blir roligare och resultaten kan du komma tillbaka till senare och faktiskt förstå vad du gjort.

Tips nummer två: Det finns nog egentligen inget bättre sätt att lära sig något än mängdträning, hur tråkigt det än låter. Oavsett om det gäller övningskörning eller matematik så gäller samma sak: öva mycket!

Extra tips (en klassiker som verkligen stämmer): En bra figur är oftast halva lösningen! Träna på att rita fint och tydligt.

Läs vidare om Mikael och spelprogrammering

• Mikaels blogg
• Bokens Hemsida

Ett område som var nytt i matematikkurserna på gymnasiet när Gy11 introducerades var det som handlar om vektorer. Tidigare har gymnasieelever framförallt läst och lärt sig om vektorer i samband med fysikkurserna men numera ingår alltså vektorer även för de elever som läser kurserna Matematik 1c och Matematik 2a. I det här blogginlägget tänkte jag att vi skulle gå igenom grunderna för att förstå en vektor och hur du även kan räkna med vektorer.

Vad är egentligen en vektor?

Om du skall förstå vad en vektor är för något så kan det vara bra att utgå från en verklig situation. Låt säga att din bil har slut på soppa och du måste be om hjälp att bli bogserad till närmsta bensinstation. Den bil som då har kopplat i bogserlinan i sin bil och därmed drar din bil kommer därmed att dra dig. I det här exemplet skulle vi kunna tänka oss att den kraft och riktning som bilen drar dig med kan visualiseras som en pil (en vektor). Den pil har både en riktning (det håll som bogserbilen drar åt) och en kraft (hur snabbt bogserbilen kör.)

En vektor beskriver alltså en storhet som både har en riktning och en storlek. Om du jämför detta med exempelvis storheter som längd eller vikt så har dessa endast en storlek.

Med hjälp av vektorer kan man beskriva en rad olika typer av storheter som kraft, acceleration eller magnetfält. Det handlar alltså om storheter som både har riktning och kraft.

Beteckning och symboler för vektorer

När man skall beteckna en vektor inom matematiken kan detta göras på lite olika vis. Det vanligaste sättet är att rita ut en pil ovanför den bokstav som betecknar vektorn. Det kan då se ut enligt

• $\vec{v}$ – Vektorn v
• $\vec{AB}$ – Vektorn med startpunkten A och slutpunkten B.

Ett annat sätt att beteckna vektorer kan vara att markera vektorn a i fet stil. I det här inlägget kommer vi att använda oss av en pil ovanför bokstaven/bokstäverna.

Rita ut en vektor

Det är mycket vanligt att man beskriver vektorer genom att rita ut dem som vektorpilar. Dels så är det ett bra sätt att förstå och räkna med vektorer men eftersom en vektor är en storhet med både kraft och riktning så är det också helt naturligt att visualisera dem genom att rita ut dem.

I bilden nedan är vektorn $\vec{AB}$ utritad. I det här fallet har vi startpunkten A och slutpunkten B för vektorn. Startpunkten A har koordinaterna (1, 2) och slutpunkten B har koordinaterna (4, 4). I bilden är även en annan vektor utritad (den gröna). Det här är faktiskt samma vektor som $\vec{AB}$ då den har samma storlek och riktning men här är startpunken flyttad till origo (0, 0). Då kan man även beskriva denna vektor endast med dess slutkoordinater (3, 2).

Det här gör alltså att även vektorn $\vec{AB} = (3, 2)$.

Addera vektorer

När man adderar eller subtraherar vektorer kan detta göras både genom använda räknelagarna för detta om man känner till koordinaterna eller genom att använda visuella metoder som parallellogrammetoden eller polygonmetoden. När man adderar två vektorer så kallas summan för resultant. D.v.s. om vi adderar $\vec{u} + \vec{v} = \vec{z}$ så kallas $\vec{z}$ för resultant.

Parallellogrammetoden

Med hjälp av den här metoden kan du beräkna resultanten och samtidigt rita ut denna. Här gör du så att du ritar ut vektorerna så att de utgår ifrån samma punkte och skapar en parallellogram där diagonalen blir resultanten för additionen mellan de bägge vektorerna.

I bilden ser du hur vektorerna $\vec{v}$ och $\vec{u}$ adderas och får resultanten $\vec{u+v}$

Polygonmetoden

Med polygonmetoden så gör du istället så att du flyttar vektorerna så att de är i följd. Resultanten blir då den vektor som har startpunkten i början av följden och slutpunkten i slutet på följden.

I bilden ovan ser du hur vektorn $\vec{a}$ flyttas till slutet på vektorn $\vec{b}$ så att vi kan rita ut resultanten $\vec{a+b}$. Den här metoden är snabbare att utföra än parallellogrammetoden om du skall addera flera vektorer än två stycken.

Räknelagar för addition och subtraktion

Om man känner till koordinaterna för vektorerna så är det enkelt att addera eller subtrahera vektorer med hjälp av de räknelagar som finns. Om vi har vektorerna $\vec{A} = (x_1, y_1)$ och $vec{B} = (x_2, y_2)$ så gäller att

• $(x_1, y_1) + (x_2, y_2) = (x_1+x_2, y_1+y_2)$
• $(x_1, y_1) – (x_2, y_2) = (x_1-x_2, y_1-y_2)$

Längden för en vektor $\vec{u}$, med koordinaterna (a, b), brukar betecknas med $| \vec{u} |$ och beräknas enligt

• $| \vec{u} | = \sqrt{a^2 + b^2}$

Det finns ett rätt kul problem inom sannolikhetsläran som kallas för Monty Hall problemet och är döpt efter en amerikansk programvärd i ett TV program som hette Lets make a deal. Problemet, som visserligen bara är löst baserat på programmet, är följande:

En programvärd ger dig möjligheten att välja mellan tre stycken olika dörrar. Bakom en av dessa dörrar finns en bil och bakom de andra två finns varsin get (?!). Du väljer först en dörr. När du valt denna dörr så öppnar programvärden en av de andra två dörrarna. Han väljer alltid en av dörrarna där det finns en get bakom denna. Frågan är nu om du skall byta dörr eller hålla kvar vid den du har valt?

OBS, Läs inte vidare härifrån om du vill fundera på svaret själv först.

Lösningen på problemet, en fråga om sannolikheter

Man tycker vid sin första tanke på problemet att det nog egentligen inte spelar någon roll om du håller fast vi den dörr som du har valt eller byter. Men saken är den att det faktiskt är högre sannolikhet att få bilen om du byter dörr. Det här kan beskrivas med hjälp av att dela upp dina val i tre stycken möjliga scenarier där två av dessa ger vinst.

1. Låt säga att du redan har valt bilen vid ditt första val. Byter du då kommer du förstås att få en get istället (vilket kanske inte är så dumt det heller) och du har förlorat.
2. Låt säga att du inte har valt bilen utan den första geten. Programledaren kommer då att öppna en av de dörrar där det finns en get. Byter du då så kommer du att välja bilen och du har vunnit.
3. Låt säga att du valde den andra geten vid ditt första val. Återigen så kommer programledaren att välja den dörr där det finns en get och byter du då så vinner du även i detta scenario.

Summa summarum, det finns alltså två av tre (2/3) scenarier där du tjänar på att byta dörr. Du ger dig alltså större sannolikhet att vinna genom att byta dörr.

Knäckte du problemet innan du hade läst förklaringen?

En tid in i inlärningen av derivata (matematik C eller matematik 3) så dyker det upp en storm av olika begrepp kopplade till derivata och kurvor.

Då stöter du säkert begreppen extrempunkter, maximipunkter, minimipunkter, terrasspunkter, extremvärden, lokala minimipunkter, lokala minimivärden, lokala maximipunkter, lokala maximivärden, globala minimivärden, globala maximivärden, globala minimipunkter, globala maximipunkter och minsta och största värde.

Pjuuh! Många begrepp helt enkelt. Det är inte konstigt om det mesta flyter ihop till en stor otillgänglig begreppsröra.

Det går förstås inte att lära sig allt på en gång. Istället får man träna och försöka se likheter och skillnader och hela tiden gå tillbaka till beskrivningar av begreppen. Det här blogginlägget tänkte jag kunde bli en bra startpunkt för detta så att du kan gå tillbaka hit och kika för att friska upp minnet när du räknar på liknande problem.

Begrepp som slutar på punkt

Låt oss först lyfta fram skillnaden på punkt och värde. En punkt är ju en koordinat med ett x – värde och ett y – värde, t.ex. (3, 4). Så när vi pratar om de olika typerna av extrempunkter nämligen maximipunkt, minimipunkt och terasspunkt så söker man eller beskriver själva punkten.

Begrepp som slutar på värde

Med värde, t.ex. olika extremvärden så är det istället y – värdet som beskrivs eller söks. Det här kallas också ibland för funktionsvärde men är alltså samma sak som y – värdet.

Maximi-, minimi- och terrasspunkter

I en maximi-, minimi- eller terrasspunkt så är antingen derivatan noll eller så befinner vi oss i ändpunkten av ett intervall.

För ändpunkten av ett intervall gäller att det är en minimipunkt om kurvan är på väg neråt och att det är en maximipunkt om kurvan är på väg uppåt. Viktigt att nämna är också att ändpunkterna av ett intervall endast kan vara en maximi eller minimipunkt om det är inkluderat, t.ex om x ≤ 3 men inte om x < 3.

Maximi och minimipunkter

Max, min och en terrasspunkt

Skillnaden på lokalt och globalt

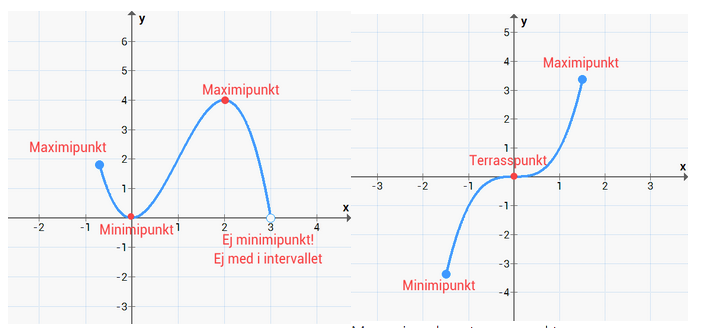
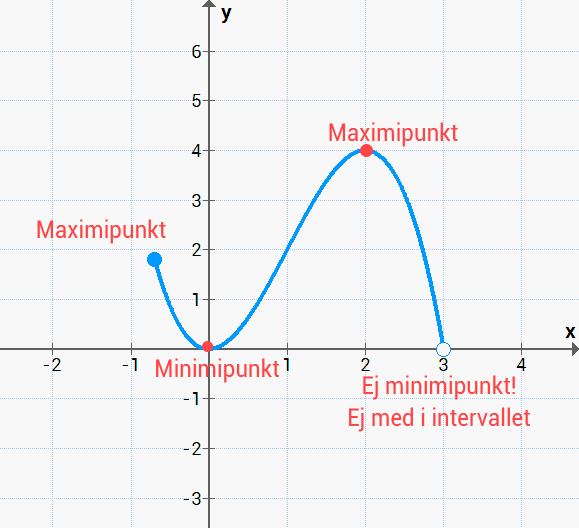
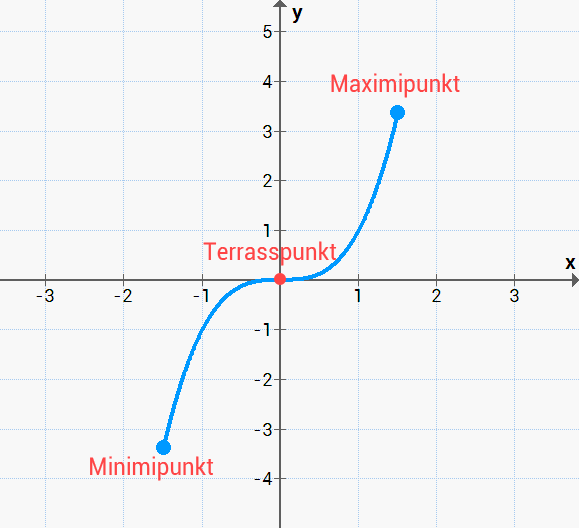
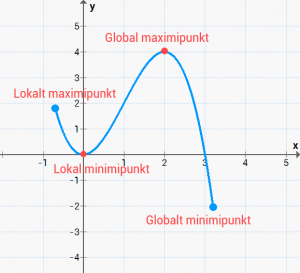För att krångla till det lite extra så finns det även lokala och globala värden/punkter. Med det här menas att man gör skillnaden på om punkten har det största y – värdet av alla extremvärden eller extrempunkter eller inte. Om punkten/värdet har det största y – värdet så är denna global, annars så är den lokal.

Lista på begrepp kopplade till Extrempunkter och Extremvärden

Kanske har du vid det här laget i alla fall en känsla för vilka olika punkter och värden som vi pratar om. För att göra det här så tydligt som möjligt så listar vi även här nedan en förklaring av alla de begrepp som vi nämnt i det här blogginlägget.

• Extrempunkt – En punkt (x, y) som är en lokal maximipunkt eller en lokal minimipunkt och där är derivatan noll. Här gäller att en terrasspunkt inte är en lokal max/min punkt och är därmed inte en extrempunkt.
• Maximipunkt – En punkt där derivatan är positiv innan punkten, noll i punkten och negativ efter. En maximipunkt kan också vara slutet av ett intervall om punkten är inkluderad i intervallet och kurvan är på väg uppåt.
• Minimipunkt – En punkt där derivatan är negativ innan punkten, noll i punkten och positiv efter. En minimipunkt kan också vara slutet av ett intervall om punkten är inkluderad i intervallet och kurvan är på väg nedåt.
• Extremvärde – Y värdet för en extrempunkt.
• Maximivärde – Y värdet för en maximipunkt.
• Minimivärde – Y värdet för en minimipunkt.
• Globalt extremvärde – Det största eller minsta y – värdet av alla extrempunkter.
• Lokalt extremvärde – Ett maximivärde eller minimivärde.
• Största värdet – Det största y – värdet i ett intervall.
• Minsta värdet – Det minsta y – värdet i ett intervall.

I gymnasieskolan råkar man ofta komma i kontakt med begreppet oändlighet vid diskussioner kring huruvida man egentligen kan dividera med noll (länk). Men det kan ju också vara intressant att diskutera hur matematiker egentligen beskriver det här begreppet.

Några tankar om oändlighet

Begreppet oändlighet är lite som en hal tvål, när man väl tror att man fått tag i den så glider den ur greppet och allt krånglas till. Det kanske även ligger i själva begreppets natur att det försöker beskriva något som vi människor (i alla fall jag) har liten möjlighet att förstå. Det enda man kan göra är att säga att det inte går att verkligen föreställa sig. Vi kan säkert föreställa oss mängden 10 genom att i huvudet rada upp 10 äpplen (eller just din favoritfrukt), lite svårare blir det att föreställa sig 100 äpplen och riktigt svårt när vi närmar oss 1000. Att rada upp oändligt antal äpplen i huvudet är helt enkelt inte rekommenderat och det finns risk för syntax error i våra fina synapser i hjärnan.

Matematikern Dedekind beskrev en oändlig mängd ungefär som att om man tar bort en mängd från denna mängd och den fortfarande är lika stor så är är den oändlig. Det är helt enkelt väldigt svårt för den mänskliga hjärnan att fånga in och bemästra begreppet.

Olika matematikers sätt att beskriva det oändliga

Ovan nämner jag matematikern Dedekinds sätt att beskriva oändlighet men självklart finns det även andra duktiga tänkare som diskuterat (om än något kontroversiellt) begreppet oändlighet. Alltifrån den grekiske matematikern Euklides till mer nutida. Man brukar faktiskt inom matematiken dela upp det här begreppet i två olika typer av oändlighet nämligen potentiell oändlighet och faktisk oändlighet.

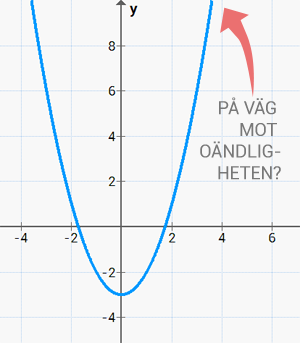Potentiell oändlighet kan sägas vara något som går mot oändligheten (växer) och kan liknas med gränsvärdet oändlighet som vi pratar om när vi beskriver derivata (länk). Du kan exempelvis tänka dig en andragradsfunktion, $f(x) = x^2$, som när x växer sig större får ett allt större funktionsvärde. Det här är också något som inte ställer till med någon större diskussion inom matematiken.

Lite mer kontroversiellt har det varit med detsom kallas för faktiskt oändlighet där man menar att oändlighet är en existerande storlek. Det var matematikern Georg Cantor som menade att det gick att beskriva oändligheter som faktiska, och till och med, olika storlekar. Det här har varit ganska kontroversiellt, inte desto mindre då han också hade viss korrespondens med den katolska kyrkan och man anar en viss koppling till det som kallas för gud.

Ett väldigt ändligt slut

Nu är det ändå hög tid att avsluta det här blogginlägget innan vi blir allt för djupa och snöar in på oändliga resonemang, jag hoppas ändå att du som kommit så här långt har fördjupat din syn något på oändligheten och lärt dig något nytt!

I klassrummet hör jag ofta ett och annat pust och stön när de nationella proven kommer på tal. Ofta så upplevs dessa prov som stora, svåröverkomliga och långa. Men istället för att förhand ge upp så är det ju bättre att kavla upp ärmarna och bestämma sig för att klara det så bra man kan. I det här blogginlägget tänkte jag ge några bra tips till dig som har bestämt dig för att lyckas så bra som möjligt.

Alla tips kanske inte passar dig men kanske något eller några kan hjälpa just dig på vägen!

1. Gör minst 2 gamla nationella prov på egen hand.

En av de viktigaste förberedelserna inför det nationella provet är att träna på tidigare utgivna nationella prov. Gör minst 2 stycken för att vänja dig vid upplägget och för att repetera kursen. Du hittar gamla nationella prov här.

2. Skriv ut och använd samma formelblad som på provet.

Det finns en bra poäng med att skriva ut och använda samma formelblad sin brukar delas ut tillsammans med de nationella proven i matte. Då vänjer du dig vid de formlerna och blir snabbare att hitta och tolka dem.

3. Skriv ner alla Begrepp och områden som ingår på provet.

Ett bra sätt att få en överblick över hela provet och kursen är att sätta sig ner någon timme och skriva ner alla områden som ingår i kursen. Känner du till de olika begreppen och formlerna som ingår i varje område? Ta annars reda på dessa.

4. Vänj dig vid att kontrollera dina svar.

Ofta kan man få någon eller några poäng på de nationella proven även fast svaret på uppgiften inte stämmer helt. Dock kan det vara onödigt att missa de poängen när man faktiskt kan kontrollera sina svar en extra gång. Ett vanligt exempel på område som är lätt att dubbelkolla svaren på är ekvationer.

5. Lär dig använda din grafritande räknare.

Många gånger går det även att kontrollera sina svar med hjälp av en grafritande räknare som är tillåtet på proven. Exempelvis kan du ta ofta ta fram närmevärden på grafritande räknare på funktioner genom att rita ut grafen, på derivata och integraler.

6. Pennan, suddet, linjalen, räknaren och kladdpappret.

Glöm dem inte, det är skönt att slippa leta efter dessa saker precis innan provet.

7. Fibrer och sömn.

Hjärnan kommer förstås att fungera bättre om du har sovit ordentligt innan och har käkat en stabil frukost. För att tänka klart så behövs det kolhydrater, även långsamma sådana som räcker länge.

8. Fastnat på en uppgift?

Även fast du förbereder dig fantastiskt bra innan provet fastnar man lätt på vissa uppgifter. Viktigt att tänka på då är att inte stanna för länge på den uppgiften. Gå istället vidare och gör de som känns lättare och återkom till den uppgiften senare när du har tid.

9. Varför en figur hjälper dig på vägen

Försök även att rita upp en figur i alla fall som det går. Då blir det lättare att förstå problemställningen och lyckas att lösa problemet.

10. Utnyttja våra gratis resurser.

Kanske du inte har en mattekurs hos oss men ändå vill kika på lite genomgångar för att förbereda dig? Kolla då igenom de lektioner hos oss som är gratis!

Slutligen önskar vi förstås dig stort lycka till!

Häromdagen satt jag och funderade på vilka filmer som jag själv har sett och där matematik på något vis har haft en central roll. Så i dagens inlägg kommer fem tips om filmer som innehåller matematik eller handlar helt om matematiker.

Något som slår mig när jag skriver ner denna lista är att många av dessa filmer också innehåller något inslag av psykologiska problem. Kombinationen av matematik, bevis och denna ingrediens verkar vara något som lockar filmskapare.

Kanske har du ett bra tips på en film som innehåller matematik? Tipsa gärna i kommentarerna!

1. Good Will Hunting

Will Hunting (originaltitel good will hunting) handlar Will, en fattig ung man som jobbar som städare på MIT och som i hemlighet är ett matematiskt geni. I filmen upptäcks han av professor Lambeau (Stellan Skarsgård) och får hjälp att ta hand om sina psykologiska problem av psykologen Maguire (spelad av Robin Williams).

Det här är ett mycket bra drama och för dig som gillar matematik finns här en hel del roliga referenser.

2. A beautiful mind

Handlar om matematikern John Nash och hans väg från att vara en ung lovande matematiker, sedan professor för att sedan få stora psykologiska problem.

Efter ett antal år med stora problem återkommer John Nash till universitetsvärlden på 1970-talet och tilldelas 1994 nobelpriset i ekonomi för sin teorier kring ämnet spelteori.

Filmen är verklighetsbaserad och huvudrollen spelas av Russell Crowe.

3. Proof

Den här filmen är inte lika känd som de två här ovan men handlar även denna om matematik (i kombination med viss sinnesförvirring). Här är det Anthony Hopkins som har placerats i rollen som den store matematiker Robert. Efter att han har dött undersöker Hal (Jake Gyllenhaal) om det inte finns gömda matematiska bevis kvar från Robert.

Han träffar då Roberts dotter Catherine (spelad av Gwyneth Paltrow) som i sin tur är lika begåvad.

4. 21

Den här filmen tar upp det vanligt återkommande temat i filmer, nämligen matematik och kortspel.

Här är det fem begåvade studenter på MIT i Usa som lär av en matematisk professor att räkna kort vid kortspelet black jack.

I rollen som matematiker spelar Kevin Spacey.

5. Andrew Wiles – Fermats sats

Slutligen ett tips som kanske inte passar lika bra in i den populärvetenskapliga hollywoodlistan här ovan. Själv tycker jag att denna dokumentär är väldigt intressant också. Mycket beroende på att dessa skapare Simon Singh är duktig på att göra så att man känner att man förstår i alla fall lite av annars mycket komplicerade teorier. Dokumentären handlar om Andrew Wiles som bevisade Fermats sista sats. Den finns för övrigt på Youtube.

Ganska ofta i gymnasiematematiken behöver du känna till att det inte går att dividera men noll. I det här blogginlägget reder vi ut varför detta inte är möjligt (odefinierat) och när du behöver tänka på detta.

Varför kan man inte dividera med noll?

För att förstå tanken bakom att division med noll är odefinierat, d.v.s. omöjligt att genomföra, kan vi försöka att se ett mönster. Vi testar att dividera 1 med mindre och mindre tal:
$\frac{1}{1} = 1$
$\frac{1}{0,1} = 10$
$\frac{1}{0,001} = 1000$
$\frac{1}{0,00001} = 100 000$
$\frac{1}{0,00000001} = 100 000 000$
$\frac{1}{0.00000000000001} = 100 000 000 000 000$

Nu förstår du säkert att om vi låter nämnaren i divisionen bli mycket litet så kommer förstås resultatet av divisionen bli mycket mycket stort. Det kommer helt enkelt att bli så stort att resultatet blir oändligt. Men vad händer då egentligen när vi dividerar med noll?

Svaret på den frågan är då helt enkelt att det inte är möjligt för det finns inget (i alla fall inte som jag känner till) som faktiskt är större än oändligheten. Flera matematiker har förstås försökt att definiera hur man faktiskt kan dividera med noll men det visar sig att detta kan leda till rätt tokiga saker. Se exempelvis den här ”ekvationen”

$a = b$ (*a)
$a^2 = ab$ ($-b^2$)
$a^2 – b^2 = ab – b^2$ (faktorisera, bl.a. med konjugatregeln)
$(a+b)(a-b) = b(a – b)$ (dividera med (a-b) )
$a+b = b$ (a = b)
$2b = b$ (/b)
$2 = 1$ (??!!)

Ser du vad som blir fel här ovan? Någonstans dividerar vi med 0…

Att hålla koll på divisionen med 0

Det är framförallt när du jobbar med rationella uttryck i exempelvis matematik 3b och 3c eller andra algebraiska uttryck som står skrivna som kvoter som du behöver hålla koll på att inte dividera med nollan. Exempelvis är ju

$\frac{x^2 + 45}{2x – 10}$

inte definierat för x = 5 då vi får 2*5 – 10 = 10 – 10 = 0 i nämnaren då. Därmed behöver vi kunna nämna att uttrycket inte är definierat för x = 5 eller att uttrycket är definerat för alla x ≠ 5.

I senare matematikkurser som matematik D och matematik 3 så börjar matteläraren helt plötsligt babbla om ett nytt vinkelmått som kallas radianer inom området trigonometri. I det här blogginlägget tänkte jag att vi skulle definiera det här begreppet och sättet att mäta vinklar så bra så att du sedan själv kan jobba vidare med det. Om du istället föredrar en video om detta så hittar du den här.

Att förstå hur radianer definieras

Tänk dig att du har en cirkel med radien 1 l.e (längdenhet) liggande på bordet framför dig. Så tar du fram din tårtspade och och skär ut en tårtbit som har den exakta båglängden 1 (se figur). Vinkeln v som då skapas definieras som 1 rad (rad = radian). Vips så har vi både fått tårta och definitionen av radianer som vinkelmått. När vi har en tårtbit med radien 1 och båglängden 1 så har vi därmed vinkeln 1 rad.

Om vi istället skär ut en tårtbit med båglängden 2 (se figur) så får vi istället vinkeln v 2 radianer.

Om vi nu skulle låta vinkeln gå hela varvet runt på enhetscirkeln så kommer båglängden att bli hela omkretsen på vår cirkel. Så hur stor är egentligen omkretsen på en cirkeln med radien 1 och diametern 2?

Eftersom vi beräknar omkretsen för en cirkel med formeln π*diameter så blir här båglängden = omkretsen π*2 = 2π. Alltså gäller att ett varv har vinkeln 2π rad.

Några vanliga vinkelmått i radianer

• 720˚ = 4π rad
• 360˚ = 2π rad
• 180˚ = π rad
• 90˚ = π/2 rad
• 45˚ = π/4 rad
• 30˚ = π/6 rad
• 1˚ = π/180 rad

Varför skall vi använda radianer istället?

Nu kanske du frågar dig varför du egentligen skall använda radianer istället för grader? Vad är egentligen meningen med det?

finns det lite olika fördelar med detta men framförallt vill vi gå över till vinkelmåttet radianer för att vi skall få en enklare, och snyggare, derivata vi derivering av trigonometriska funktioner. Det visar sig nämligen att när man deriverar trigonometriska funktioner, t.ex. f(x) = cos x och f(x) = sin x, så får vi krångligare uttryck med grader än med radianer.

Från grader till radianer och tillbaka igen

Kanske du nu känner att du både har förstått radianer och vet varför vi egentligen skall använda oss av detta vinkelmått istället och är redo för lite räkneexempel. Låt oss börja att ta några exempel där vi går från grader till radianer och vice versa. Viktigt att känna till när du jobbar med dessa omvandlingar är att 1˚ = π/180 rad.

• 55˚ = 55 * (π/180) = 55π/180 = 11π/36 rad
• 120˚ = 120 * (π/180) = 120π/180 = 2π/3 rad
• π/9 = 180/9 = 20˚
• 2π/5 = 360/5 = 72˚

Träna gärna själv nedan på att göra dessa omvandlingar.

Trigonometriska ekvationer och radianer

Det är framförallt bra att ha koll på att ett helt varv är 2π radianer, ett halvt π radianer och att 90˚ = π/2 radianer när du löser ekvationer och skall svara med radianer i svaret. Det som spelar roll här är att du alltid måste ange periodiciteten för alla lösningar till en ekvation då dessa återkommer om och om igen för sin, cos och tan. Periodiciteten för sin och cos är 360˚ (2π rad) och för tan 90˚ (π/2 rad).

Låt oss ta ett exempel på detta.

Lös ekvationen sin 2x = 0,5
$sin 2x = 0,5 \Leftrightarrow$
$2x = \frac{ pi }{ 6 } + n \cdot 2 \pi \Leftrightarrow$
$x = \frac{ pi }{ 12 } + n \cdot \pi$
eller
$2x = \pi – \frac{ pi }{ 6 } + n \cdot 2 \pi \Leftrightarrow$
$x = \frac{ 5 pi }{ 12 } + n \cdot pi$