Vi har tidigare intervjuat en del människor som tidigare pluggat matte, forskar eller på något annat vis har en koppling till att plugga matematik på gymnasiet. För ett tag sedan fick jag ett mail från Marcus Näslund med många intressanta tankar och idéer om varför det är så viktigt koppla ihop matematiken med hur den används i verkligheten. Efter lite mailkonversation tyckte jag att det vara lika bra att göra en intervju med Marcus om hans tankar om matematik och framförallt att han kunde berätta lite mer om den bok han just nu håller på att skriva på – ”Verklighetens Kvadratrötter”
– Berätta lite om dig själv och din bakgrund
Jag heter Marcus Näslund och läser för närvarande Kandidatprogrammet i Matematik vid Uppsala Universitet, men är född och uppvuxen i Dalarna. Mina stora intressen utöver fotboll och simning är teknik och naturvetenskap i allmänhet. Teknik och datorer har fascinerat mig genom hela livet och har stimulerat mig till att konstant undra över varför saker är som de är. Datorer gör som de gör för att de programmerade så. Programmeringsspråken resulterar i vad de gör för att kretskorten ser ut på ett sätt. Kretskorten beter sig som de gör för att elektriciteten beter sig som den gör. Elektriciteten beskrivs av fysikaliska lagar, som uttrycks och analyseras matematiskt. Oavsett område så kommer man alltid till matematiken, om man funderar tillräckligt länge. Jag ville verkligen förstå, inte bara datorerna utan allting annat om världen, och då hamnade jag till slut i matematikens domäner. Jag jobbar också mycket på olika populärvetenskapliga event såsom Polhem Scifest, Teknikåttan samt på Mattecentrums räknestugor.
– Vad tyckte du om att läsa matematik på gymnasiet?
Min egen upplevelse var nog rätt speciell, då jag fick började med gymnasiets kurser på högstadiet och högskolekurser under mitt tredje gymnasieår. Men jag vet mycket väl hur det kan vara och hur mina klasskamrater hade det.
Gymnasiematten är gjord på ett väldigt tråkigt sätt som gör att den ger intryck av att matematik är ett tråkigt ämne, snarare än att bara skolmatematiken är det. Det talas alltför lite (eller ofta inget alls) om vad matematik egentligen är, det vill säga försök att logiskt resonera kring det allra mest grundläggande i universum (och bortom det). Det talas inte heller om vad dessa kunskaper används till, vare sig inom vardagen eller inom olika tekniker, vilket då Verklighetens Kvadratrötter förhoppningsvis kan råda lite bot på.
Det finns ju olika bra och dåliga lärare, men i allmänhet reduceras matematik på gymnasiet helt enkelt till att lyssna till en lärare och räkna ut olika abstrakta tal i en bok, där det rätta svaret finns längst bak. Helt utan någon anknytning till andra ämnen eller till verkligheten. Då är det ju inte så konstigt om elever inte blir intresserade eller att den allmänna uppfattningen är att matematik är tråkigt.
– Hur fick du idén till att skriva en bok om hur matematik kan kopplas ihop med konkreta situationer?
När folk frågar vad man sysslar med har svaret ”plugga till matematiker” en förmåga att helt döda konversationen. Men så bör det ju självklart inte vara, folk vet helt enkelt inte tillräckligt mycket om ämnet. De förknippar matematik med den skolmatematik jag talade om innan, något väldigt tråkigt och oanvändbart.
Får jag en chans att prata om användningsområden, vad jag faktiskt sysslar med om dagarna och vad som driver mig i mina studier, så blir det plötsligt fascinerande. Med all rätt, nog kan inte något så allomspännande och viktigt (det har trots allt förundrat människor i tusentals år) vara tråkigt? Det motiverar mig mycket för denna bok – att få en möjlighet att ändra uppfattningen och kunna förklara varför man som jag vill syssla med matematik.
– Varför tror du att det kan vara viktigt att koppla ihop det teoretiska ämnet matematik med konkreta situationer och exempel?
Matematik är ett mycket abstrakt och teoretiskt ämne, men det är viktigt att visa att detta inte gör det tråkigt eller oanvändbart. Tvärtom är det precis den abstrakta och generella natur som matematik har gör den extremt användbar, eftersom resultat kan appliceras på jättemånga områden och inte bara ett specifikt.
Tyvärr talas det inte så mycket om användningsområden på högstadiet eller i gymnasiekurserna, vilket jag tycker man borde. Det inger en viss känsla för hur viktig matematiken faktiskt är för oss. Idag kanske mer än någonsin, när teknik och genomsyrar hela samhället och matte och logik ju faktiskt är datorernas språk.
– Vilket är ditt egna favoritexempel på där matematik verkligen kommer till användning?
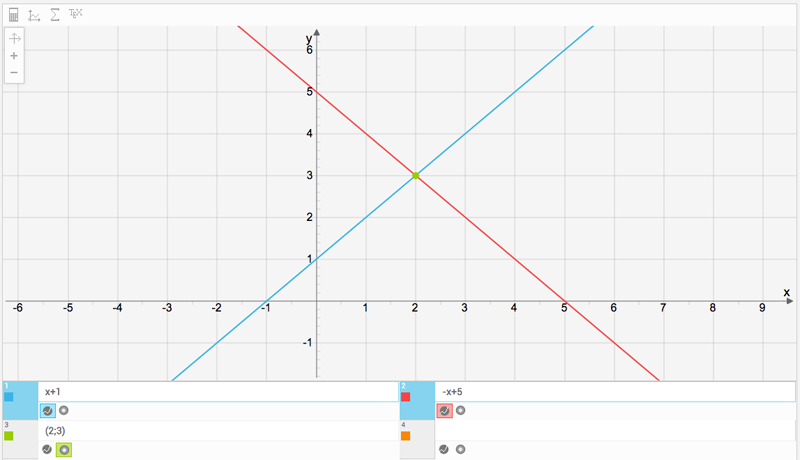
Ekvationssystem är något som man vidrör lite lätt under gymnasiet men inte gör så mycket mer med. Men det är precis sådana som en GPS använder använder för att ta reda på ens position och sedan kunna visa det på en karta. De obekanta x, y och z används i enstaka ekvationer för att beskriva förhållandet mellan en själv och olika GPS-satelliter. Med tillräckligt många ekvationer i systemet kan dessa obekanta lösas ut och ger då ens egen position – oerhört vackert.
En annan favoritgrej är primtal (som kanske inte diskuteras i gymnasiet, TYVÄRR) och studier av dessa och övriga tal, som i matematiken kallas talteori. De till synes oanvändbara begreppen används inom kryptering, för att skydda information, på exempelvis kreditkort och när man handlar på Internet. Det (RSA-kryptering) är också en riktig matematisk skönhet.
Båda beskrivs naturligtvis i boken, tillsammans med saker som datorspelsgrafik, statistik, medicin, bild- och filmkomprimering, energtillverkning, rymdutforskning, arkitektur, radioaktivitet, väderförutsägelser, Googlesökningar och olösta matematiska problem.
– Om du skulle ge några tips till de som kämpar med matten på gymnasiet idag, vilka skulle det vara?
I alla ämnen tror jag det är viktigt att hitta något som driver en själv. Självklart blir inte alla matematiker och alla har inte samma djupa intresse för ämnet. Däremot har alla ett behov av att kunna tänka logiskt, vilket är en avsedd bieffekt av att studera matematik. I många fall, inte minst inom vardagliga ämnen som ekonomi och statistik, behövs också en del rena matematikkunskaper, varför det är viktigt att vara öppen och låta sig inspireras av detta ämne.
För min del är det teknik i olika områden och alla möjliga fascinerande tillämpningsområden som först motiverade mig till att studera matematik på högre nivå. Är det något man tycker om ska man försöka ta reda på mer om sådant. Verklighetens Kvadratrötter är då ett självklart tips, och jag hoppas att det ska kunna väcka intresset eller åtminstone förståelsen för matematik hos matematikelever men även hos mattelärare.