Start / Logaritmer
Logaritmer
Allt om logaritmer
En logaritm används till att lösa exponentialfunktioner. Vanliga logaritmer är tiologaritmen och den naturliga logaritmen. Här samlar vi alla lektioner om logaritmer hos Eddler.
Våra lektioner om logaritmer
Här hittar du alla lektioner hos oss som handlar om logaritmer.
Tiologaritmen Videolektion
Matematik 2c, Matematik 2b, Matematik 2a, Matematik 2Exponentialekvationer Videolektion
Matematik 2a, Matematik 3c med Avancera I, Matematik 2Lösa exponentialekvationer med logaritmer Videolektion
Matematik 2c, Matematik 2b, Matematik 2a, Matematik 3c med Avancera I, Matematik 2Logaritmlagarna och logaritmekvationer Videolektion
Matematik 2c, Matematik 3c med Avancera I, Matematik 2Talet e och den naturliga logaritmen ln Videolektion
Matematik 3c, Matematik 3b, Matematik 3c med Avancera I, Matematik 3Mer om logaritmer
Logaritmer är ett sätt att hantera exponenter så att du kan lösa exponentialekvationer. Vi kan se logaritmen som en invers till en exponentialfunktion.
Vi beskriver logaritmer på tre olika sätt. Först med en formel, därefter med vanligt språk och slutligen med en graf.
Med andra ord står det här ovan i formeln att ”logaritmen av ett tal b är den exponent x man måste upphöja basen a till, för att få talet b”.
Det kan vara svårt i början att förstå vad detta egentligen innebär. Därför är det viktigt att vi presenterar samma information med hjälp av en bild.
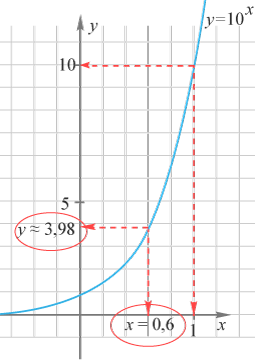
Här ovan är grafen till utritad. Det tal vi upphöjer 10 med för att få ungefär 2,98 är 0,6. Därför är log(3,98) = 0,6. Med andra ord betyder det att det tal vi upphöjer 10 med för att 3,98 är log(3,98). Om du fortfarande upplever att detta är svårt att förstå rekommenderar vi att du går in i vår videolektion om logaritmer.
Det finns dessutom några viktiga regler för logaritmer. Exempelvis behandlar dessa regler hur du adderar och subtraherar logaritmer.
Lösa exponentialekvationer
Det viktigaste användningsområdet för logaritmer är att lösa exponentialekvationer. Därför visar vi ett enkelt exempel här nere.
Lös ekvationen
Vi börjar med att logaritmera bägge leden.
Vi använder logaritmlag
Dela bägge leden med
Det sista steget räknades ut med räknarens log funktion.
Olika typer av logaritmer
De exempel som visades här ovan räknades ut med hjälp av tiologaritmen. Dessutom finns det fler logaritmer som ofta används. Ett exempel på en sådan logaritm är ln, den naturliga logaritmen. Den använder talet e som bas istället för 10. Egentligen är vi inte begränsade till att använda talet 10 eller talet e som bas. Vi använder egentligen vilket tal som som helst som tal.
Ämnesplaner (skolverket)
Höj dina resultat i matematikkursen!
- Högstadiet och hela gymnasiet.
- Mer än 600 supertydliga videos.
- Träna inför ditt nationella prov.
- Dessutom Fysik 1, programmering och högskoleprovet.
Nyheter
Nya lektioner med tips om provdelen KVA, se mer i vår Högskoleprovskurs.
Populära kurser
Åk 9
66 lektioner

Matematik 2b
92 lektioner

Matematik 3c
67 lektioner

Högskoleprovet
71 lektioner

Matematik basår
95 lektioner

Fysik 1
92 lektioner
Våra användare gillar oss!
Populära lektioner
Räta linjens ekvation Gratis
Matematik 2
Ekvationslösning
Matematik 1
Vad är Algebra?
Matematik 1
Beteckningen f(x)
Matematik 1
Ohms lag Gratis
Fysik 1
Förenkla algebraiska uttryck
Matematik 1
Tallinjen Gratis
Matematik 1
Vad är funktioner
Matematik 1
Kort division - dividera med uppställning
Matematik högstadiet
Enhetscirkeln Gratis
Matematik 3
Få tillgång till allt för
endast 99 kr/mån
Över 600 lektioner. Ingen bindningstid. Avsluta när du vill.
Prova gratis