Start / Rationella uttryck
Rationella uttryck
Allt om rationella uttryck
Ett rationellt uttryck är en kvot av två polynom. På samma vis som ett bråktal har en täljare och en nämnare så har även ett rationellt uttryck det. Här samlar vi alla våra lektioner och resurser om rationella uttryck.
Våra lektioner om rationella uttryck
Här hittar du alla lektioner hos oss som handlar om rationella uttryck.
Vad är ett rationellt uttryck? Gratis Videolektion
Matematik 3c, Matematik 3b, Matematik 3c med Avancera I, Högskoleprovet matematik, Matematik 3
Förenkla rationella uttryck Gratis Videolektion
Matematik 3c, Matematik 3b, Matematik 3c med Avancera I, Högskoleprovet matematik, Matematik 3
Addition och subtraktion av rationella uttryck Videolektion
Matematik 3c, Matematik 3b, Matematik 3c med Avancera I, Högskoleprovet matematik, Matematik 3
Multiplicera och dividera rationella uttryck Videolektion
Matematik 3c, Matematik 3b, Matematik 3c med Avancera I, Högskoleprovet matematik, Matematik 3
Vad är ett polynom? Gratis Videolektion
Matematik 3c, Matematik 3b, Matematik 3c med Avancera I, Matematik 3
C och A uppgifter på rationella uttryck Videolektion
Matematik 3c, Matematik 3b, Matematik 3Mer om rationella uttryck
Rationella uttryck ingår i kurserna Matematik 3b och 3c. Det är en fördjupning av den algebra som du lär dig i Matematik 2 och en viktig förberedelse inför områden som derivata och integraler.
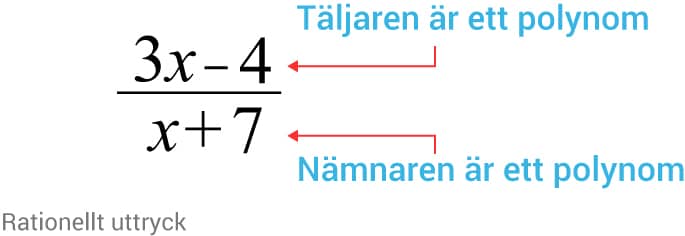
När vi definierar ett rationellt uttryck så gör vi det på följande vis.
Definition
Ett rationellt uttryck $R(x)$ är en kvot av två polynom $P(x)$ och $Q(x)$.
$R(x)=\frac{P(x)}{Q(x)}$
där $Q(x) \ne 0$
Du lär dig mer om hur ett rationellt uttryck definieras och när det inte är definierat i den här lektionen. Kortfattat så är det viktigt att du vet att nämnaren inte får vara lika med 0. Det beror på att division med 0 inte är definierat.
Exempelvis är uttrycket $\frac{xy^2}{x+1} $ inte definierat då $x=-1$. Om du sätter in det x-värdet i nämnaren så får du nämligen 0.
Som förförståelse till detta är det viktigt att kunna hantera bråk och grundläggande algebra. Därefter blir det enklare att jobba med lite mer avancerad algebra.
Förenkla och utveckla rationella uttryck
När du förstår vad ett rationellt uttryck är så är nästa steg att kunna hantera algebran kring uttrycken. Exempelvis kan du förenkla rationella uttryck, addera och subtrahera rationella uttryck samt dividera och multiplicera dem.
För att visa hur detta ser ut så tar vi två exempel där vi förenklar och utvecklar rationella uttryck.
Förenkla $\frac{x^2y^3}{x} $
Lösning
Här förkortas uttrycket med $x$
$\frac{x^2y^3}{xy}=\frac{x \cdot x \cdot y \cdot y \cdot y}{xy}=xy^2$
Utveckla och förenkla $\frac{x^2y^3}{x} \big/ \frac{1}{x} $
Lösning
Här använder vi regeln för att dividera rationella uttryck
$\frac{x^2y^3}{x} \big/ \frac{1}{x} =\frac{x \cdot x^2y^3}{x} = x^2y^3$
Ämnesplaner (skolverket)
Höj dina resultat i matematikkursen!
- Högstadiet och hela gymnasiet.
- Mer än 600 supertydliga videos.
- Träna inför ditt nationella prov.
- Dessutom Fysik 1, programmering och högskoleprovet.
Nyheter
Nya lektioner med tips om provdelen KVA, se mer i vår Högskoleprovskurs.
Uppdaterade lektioner om Trigonometri i Ma 4. Se dem i kursen.
Lektioner och kurser hos oss
Utforska våra kurser. Flera av våra populära lektioner är helt gratis.
Populära kurser
Åk 9
66 lektioner
Matematik 2b
92 lektioner
Matematik 3c
67 lektioner
Högskoleprovet
71 lektioner
Matematik basår
95 lektioner
Fysik 1
92 lektioner
Våra användare gillar oss!
Populära lektioner
Räta linjens ekvation Gratis
Matematik 2
Ekvationslösning
Matematik 1
Vad är Algebra?
Matematik 1
Beteckningen f(x)
Matematik 1
Ohms lag Gratis
Fysik 1
Förenkla algebraiska uttryck
Matematik 1
Tallinjen Gratis
Matematik 1
Vad är funktioner
Matematik 1
Kort division - dividera med uppställning
Matematik högstadiet
Enhetscirkeln Gratis
Matematik 3
Få tillgång till allt för
endast 99 kr/mån
Över 600 lektioner. Ingen bindningstid. Avsluta när du vill.
Köp Premium Prova gratis