Start / Andragradsekvationer
Andragradsekvationer
Allt om andragradsekvationer
En andragradsekvation är en ekvation som innehåller termen $x^2$. Allmänt kan en sådan ekvation skrivas på formen $ax^2+bx+c=0$. Nedan samlar vi alla våra lektioner och resurser så att du kan lära dig att lösa andragradsekvationer.
Våra lektioner om andragradsekvationer
Här hittar du alla lektioner hos oss som handlar om andragradsekvationer.
Vad är en Andragradsekvation Gratis Videolektion
Matematik Nivå 2c, Matematik Nivå 2b, Matematik Nivå 2a, Matematik 2c, Matematik 2b, Matematik 2a, Matematik 3c med Avancera I, Högskoleprovet matematik, Matematik 2
Roten ur – Andragradsekvationer Videolektion
Matematik Nivå 2c, Matematik Nivå 2b, Matematik Nivå 2a, Matematik 2c, Matematik 2b, Matematik 2a, Matematik 2
Nollproduktmetoden Videolektion
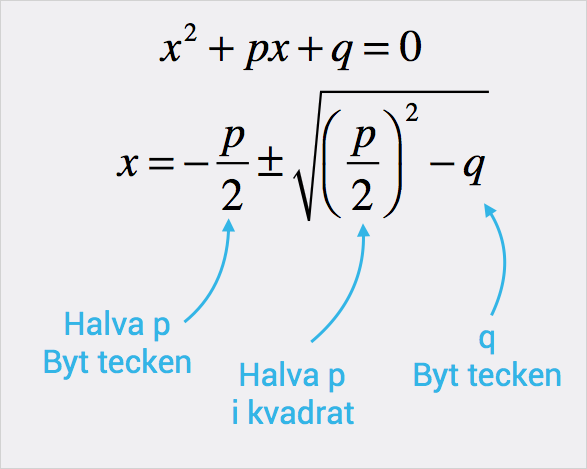
Matematik Nivå 2c, Matematik Nivå 2b, Matematik Nivå 2a, Matematik 2c, Matematik 2b, Matematik 2a, Matematik 3c med Avancera I, Matematik 2
PQ – formeln Gratis Videolektion
Matematik Nivå 2c, Matematik Nivå 2b, Matematik Nivå 2a, Matematik 2c, Matematik 2b, Matematik 2a, Matematik 3c med Avancera I, Högskoleprovet matematik, Matematik 2
Träna mera på PQ-formeln Videolektion
Matematik Nivå 2c, Matematik Nivå 2b, Matematik Nivå 2a, Matematik 2c, Matematik 2b, Matematik 2a, Matematik 2
Rotekvationer Videolektion
Matematik Nivå 2c, Matematik 2c, Matematik 2
Kvadratkomplettering Videolektion
Matematik Nivå 2c, Matematik Nivå 2b, Matematik Nivå 2a, Matematik 2c, Matematik 2b, Matematik 2a, Matematik 3c med Avancera I, Matematik 2
Andragradsekvationer med komplexa rötter Videolektion
Matematik Nivå 2c, Matematik 2c, Matematik 2
Andragradsekvationer och problemlösning Videolektion
Matematik Nivå 2c, Matematik Nivå 2b, Matematik Nivå 2a, Matematik 2c, Matematik 2b, Matematik 2a, Högskoleprovet matematik, Matematik 2Mer om andragradsekvationer
Den allmänna formeln för att beskriva andragradsekvationer är $ax^2+bx+c=0$ där $a$, $b$ och $c$ är konstanter. För att det skall vara en andragradsekvation så måste ekvationen innehålla termen $x^2$. Därför måste $a$ vara skilt från 0.
Du använder några olika lösningsmetoder för dessa typer av ekvationer. De tre vanligaste är kvadratrotsmetoden, nollproduktmetoden och pq-formeln. Med andra ord så väljer du en passande metod beroende på hur ekvationen ser ut. Du kan läsa mer om hur du väljer metod genom att gå till vår lektion om detta.
Ekvationen $x^2-4=0$ är en andragradsekvation vi kan lösa med roten ur.
$x^2-4=0$
Addera bägge leden med $4$
$x^2=4$
Ta roten ur i bägge leden
$x=\pm\sqrt{4}=\pm2$
Lösningarna är
$\begin{cases} x_1=2 \\ x_2=-2 \end{cases}$
Rotekvationer och komplexa rötter
Det finns speciella fall av andragradsekvationer som du också behöver känna till. Exempelvis kallas vissa andragradsekvationer för rotekvationer. Du behöver kvadrera bägge leden när du löser sådana ekvationer. Dessutom behöver du testa lösningarna extra noggrant då de kan innehålla falska rötter.
Ett annat fall är när ekvationen har komplexa rötter. Du möter detta när du ser att du behöver ta roten ur ett negativt tal.
Andragradsekvationen $x^2=-4$ har komplexa rötter.
$x^2=-4$
Ta roten ur i bägge leden
$x=\pm\sqrt{-4}=\pm2i$
Lösningarna är
$\begin{cases} x_1=2i \\ x_2=-2i \end{cases}$
Andragradsekvationer och andragradsfunktioner
Dessa typer av ekvationer kopplas även samman med andragradsfunktioner i Matematik 2. Därför är det viktigt att du lär dig att lösa dessa ekvationer innan eller under tiden som du lär dig om de funktionerna.
Skillnaden mellan en ekvation och en funktion är att en ekvation är en likhet mellan ett vänsterled och ett högerled där något okänt söks. Funktioner, däremot, är ett samband mellan två variabler. Exempelvis beskrivs detta samband ofta med en tabell eller en graf.
Ämnesplaner (skolverket)
Höj dina resultat i matematikkursen!
- Högstadiet och hela gymnasiet.
- Mer än 600 supertydliga videos.
- Träna inför ditt nationella prov.
- Dessutom Fysik 1, programmering och högskoleprovet.
Nyheter
Nya lektioner med tips om provdelen KVA, se mer i vår Högskoleprovskurs.
Lektioner och kurser hos oss
Utforska våra kurser. Flera av våra populära lektioner är helt gratis.
Populära kurser
Åk 9
66 lektioner
Matematik 2b
92 lektioner
Matematik 3c
67 lektioner
Högskoleprovet
71 lektioner
Matematik basår
95 lektioner
Fysik 1
92 lektioner
Våra användare gillar oss!
Populära lektioner
Räta linjens ekvation Gratis
Matematik 2
Ekvationslösning
Matematik 1
Vad är Algebra?
Matematik 1
Beteckningen f(x)
Matematik 1
Ohms lag Gratis
Fysik 1
Förenkla algebraiska uttryck
Matematik 1
Tallinjen Gratis
Matematik 1
Vad är funktioner
Matematik 1
Kort division - dividera med uppställning
Matematik högstadiet
Enhetscirkeln Gratis
Matematik 3
Få tillgång till allt för
endast 99 kr/mån
Över 600 lektioner. Ingen bindningstid. Avsluta när du vill.
Köp Premium Prova gratis