De allra flesta är vana att skicka ut en massa emojis när vi skickar meddelanden till varandra via mobilen. Men har du någon gång provat att lösa emoji-matteproblem? I det här blogginlägget har jag skapat tre kluringar där man skall ta reda på vilket tal som döljer sig bakom en eller flera emojis. Det finns tre problem och tanken är att de skall vara i stigande svårighetsgrad.
Du hittar förklaringar till varje problem längst ned där jag också går igenom vilken matematik som du kan använda för att lösa liknande problem.
Emojikluring 1

Målet är att du skall ta reda på vad (tungan)-(tigern) är lika med.
Emojikluring 2
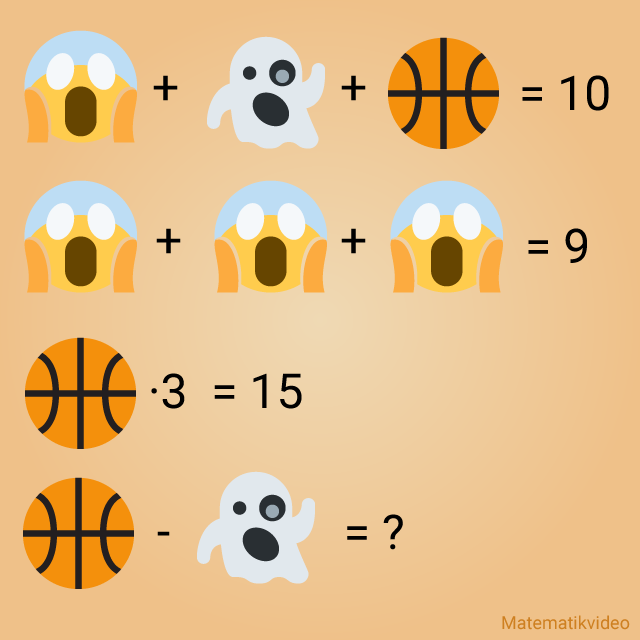
I den här kluringen skall du ta reda på vad (bollen)-(spöket) är lika med.
Emojikluring 3
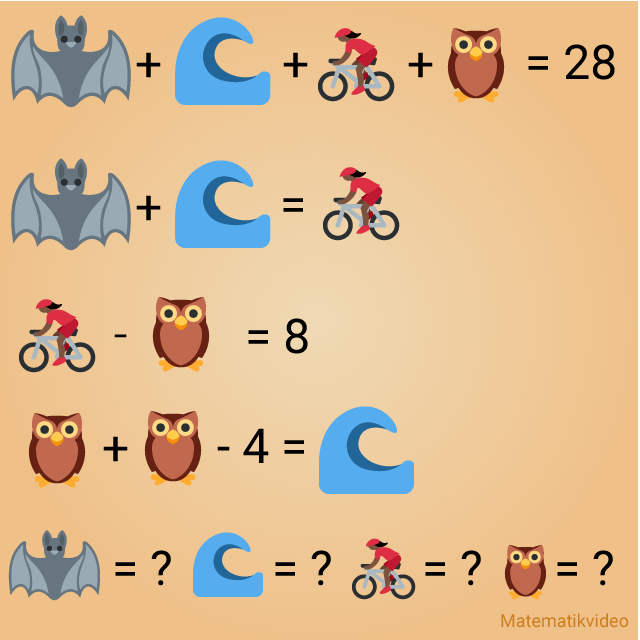
Här skall du ta reda på vilka tal som döljer sig bakom alla emojis. Det här problemet är lite klurigare men det finns genvägar, hittar du dem?
Förklaringar och rätta svar
När du har kommit så här långt har du säkert kommit fram till något svar på ovanstående problem. Du vill förstås säkert veta att du har gjort och tänkt rätt? Nedan så presenterar jag de rätta svaren och ett sätt att lösa varje problem på. Kanske har du hittat en annan väg än vad jag har gjort? Kommentera gärna hur du då tänkte.
Lösning emoji 1

Korrekt svar här är 0.
Du kan börja med mittenraden där du får reda på att (tiger)-1=1. Då vet du att (tiger)=2.
Sedan använder du den första raden för att ta reda på (munnen). Du vet att (tiger)=2 och att (mun)+(tiger)=4 som vi kan skriva som (mun)+2=4, alltså är (mun)=2.
Nu använder vi sista raden och beräknar (mun)-(tiger) = 2-2 = 0.
Lösning emoji 2
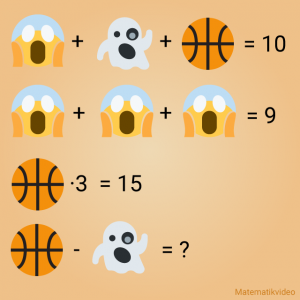
Korrekt svar är 3.
Här kan vi börja på rad 2 där vi har (Screaming face)+(Screaming face)+(Screaming face)=9. Alltså måste (Screaming face)=3.
På rad 3 har vi (boll)·3=15 vilket ger att (boll)=5.
Nu använder vi rad 2 och rad 3 för att genom rad 1 ta reda på (spöket). Vi sätter in det vi vet och får att 3+(spöke)+5 = 10. Alltså är (Spöke)=10-8=2.
Slutligen beräknar vi (boll)-(spöke)=5-2=3.
Lösning emoji 3
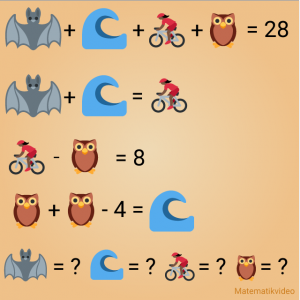
Korrekt svar: (fladdermus)=8, (våg)=4, (cyklist)=12, (uggla)=4
Det här är nog den klurigaste av de tre men det finns lite av en genväg här så att du slipper sitta med ett större ekvationssystem.
1) På rad 2 ser vi att (fladdermus)+(våg)=(cyklist).
2) På rad 3 ser vi att (cyklist)-(uggla)=8, alltså gäller att (uggla)=(cyklist)-8.
Nu sätter vi in det vi vet från 1) och 2) i rad 1 så att vi får att
(fladdermus)+(våg)+(cyklist)+(uggla)=(cyklist)+(cyklist)+(cyklist)-8=28
Vi förenklar detta så att vi har
3·(cyklist)-8=28
3·(cyklist)=36
(cyklist)=36/3=12
Nu har vi (cyklist) och kan ta reda på ugglan. Från rad 3 får vi att 12-(uggla)=8, dvs (uggla)=4
Nu har vi (uggla) och kan ta reda på (våg) från rad 4. Vi får där att 4+4-4=(våg), dvs (våg)=4.
Slutligen kan vi ta reda på (fladdermus) från rad 1 eller 2. Jag väljer att från rad 2 använda att (fladdermus)+4=12, dvs (fladdermus)=8.
Klart 🙂 ;-D 😀
Vilken matematik kan man använda för liknande problem?
När jag förklarar problemen här ovan använder jag inte man faktiskt skulle kunna byta ut emojis mot variabler som $x$x, $y$y eller $z$z. Om vi skulle göra det så skulle vi få en uppsättning av två eller flera ekvationer. Detta kallas i matematiken för linjära ekvationssystem och det ingår framförallt i gymnasiets kurs Matematik 2abc i området linjära funktioner. Då använder man oftast att man ersätter det okända med variabler och löser sedan ekvationssystemet med metoder som additionsmetoden eller substitutionsmetoden. Här ovan så skriver jag inte ut det men det är substitutionsmetoden som används där. Dvs att jag byter något (substituerar) i den ena ekvationen mot något i den andra för att ta reda på lösningarna. Vill du veta mer om detta så rekommenderar jag att du kör igång med Matte 2 hos oss där vi har mycket sådan teori med exempel och övningar.
Även om man inte har jobbat med dessa matematiska områden så skulle jag vilja påstå att man ändå kan lösa dessa problem. Det är ju märkligt hur mycket mer lösbart ett problem kan bli om man plockar bort algebraiska tecken och variabler. Med logik kring de här bilderna så kan man lösa dessa problem ändå 🙂
Hur gick det för dig med problemen?

Med vänlig hälsning
Simon Rybrand