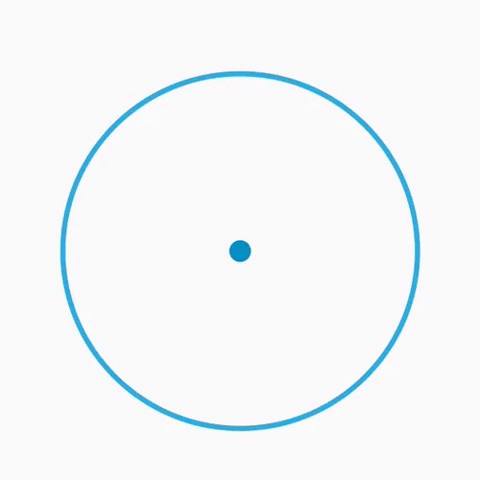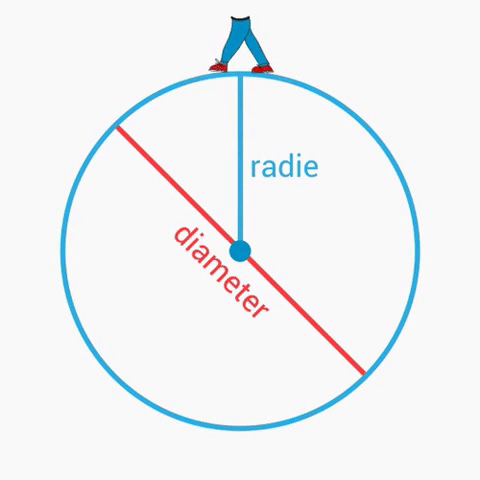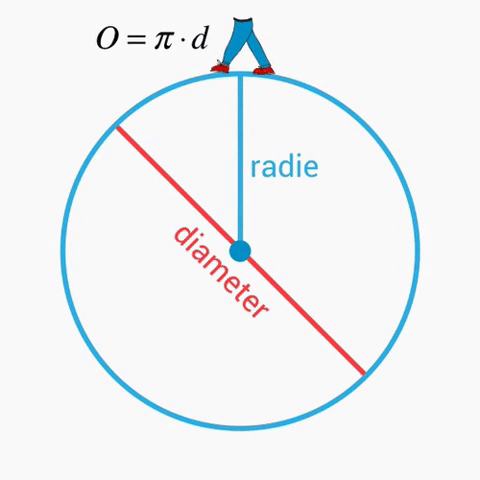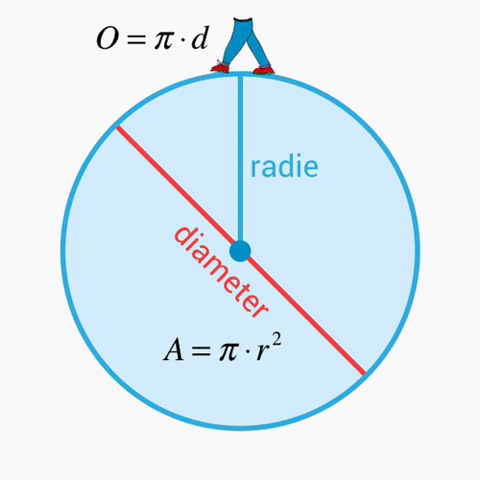
Ska du skriva högskoleprovet nu i vår 2017 och funderar på hur du bäst och snabbast förbereder dig?
Här hjälper vi dig på vägen och samlar ihop några effektiva tips som förbättrar dina matematikfärdigheter inför provet.
Vilka matematikområden är viktigast att plugga på?
I de så kallade kvantitativa delarna (Matematik och statistik) på högskoleprovet så är det framförallt gymnasiets kurs Matematik 1b som utgör grunden.
Personligen brukar jag dock säga att det är rätt bra att även plugga på räta linjens ekvation, algebran, linjära ekvationssystem från Matematik 2 och i alla fall kika på rationella uttryck från Matematik 3. Alla delar som vi rekommenderar att kunna hittar du förstås i vår Högskoleprovskurs.
Testa en HP lektion direkt
För dig som vill se mer specifika matematikområden att plugga på så kan du kika in i det här blogginlägget med tips om XYZ. Tipsen där gäller även för alla matematikdelar på provet.
Hur tränar man upp sin snabbhet?
För att träna upp sin snabbhet så är det viktigaste att vara trygg med de matematiska grunderna och sedan träna på gamla högskoleprov. Sedan kan du fortsätta och träna ännu mer på gamla högskoleprov och krydda med lite träning på huvudräkningsstrategier och överslagsräkning.
Om du vill dyka ner i sådan tekniker och strategier så har vi skrivit om detta när vi tipsade om DTK delen för ett tag sedan här på bloggen. Där hittar du några riktigt bra tips på det här temat.
Hur är man lugn och metodisk på ett prov?
Ett av de allra viktigaste verktygen för att lyckas på ett prov är att hantera sina känslor kring provet. Många blir naturligtvis nervösa när man skriver ett prov. Potentiellt kan ju högskoleprovet betyda att man kommer in på sin drömutbildning eller inte. Men det finns sätt att hantera sin oro och nervositet!
De allra flesta tycker att kunskaperna känns självklara att träna på inför provet, inte så många pratar om alla de känslor man upplever innan, under och efter provet. Det har visat sig att det fungerar rätt bra att skriva om dessa känslor för att kunna hantera dem.
”By writing down one’s negative thoughts, students may come to realize that the situation is not as bad as they thought or that they are prepared to take it on,” said Beilock, an associate professor of Psychology at the University of Chicago.
”As a result, they worry less during the test.”
Vi har tidigare skrivit om just oro och rädslor kring prov i följande två blogginlägg:
För dig som känner så här så rekommenderar vi att du läser igenom detta.



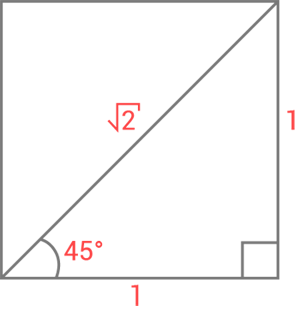
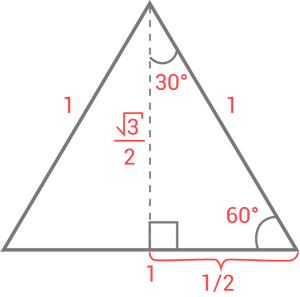
 Varför gick duvan över Möbiusbandet?
Varför gick duvan över Möbiusbandet? Tre statistiker gick ut för att jaga tillsammans. Efter en stund så får de syn på en kanin. Den första statistikern skjuter på kaninen men missar och skjuter över. Den andra statistiken skjuter nu istället men skjuter under kaninen. Den tredje statistikern utbrister då ”Jaaa! Vi fick den!”.
Tre statistiker gick ut för att jaga tillsammans. Efter en stund så får de syn på en kanin. Den första statistikern skjuter på kaninen men missar och skjuter över. Den andra statistiken skjuter nu istället men skjuter under kaninen. Den tredje statistikern utbrister då ”Jaaa! Vi fick den!”. I matematiken finns de tre sorgligaste kärlekshistorierna, dessa tre är:
I matematiken finns de tre sorgligaste kärlekshistorierna, dessa tre är: