Hur svårt är det tekniska eller naturvetenskapliga basåret?

Jag har svårt med Matematik – Hur gör jag?

69 Svar

Lite då och då får jag ett e-postmeddelande där någon undrar hur man kan komma igång med sina matematikstudier trots att denne definierar sig själv som en någon som har svårt för matematik.

Jag kände därför att jag ville försöka lyfta just den här frågan i hopp om att nå ut till några till som kämpar med just de här sakerna. Själv tror jag nämligen att alla de allra flesta kan klara gymnasiekurserna i matematik, bara det finns en vilja till detta. Det behöver nödvändigtvis inte bli helt smärtfritt men det går.

Jag började skriva ett blogginlägg om det här men märkte snabbt att det blev mer och mer text och för att försöka göra det så överskådligt som möjligt så delade jag istället upp det i 3 stycken olika blogginlägg som jag tänkte publicera över den närmaste tiden.

I det här första blogginlägget tänkte jag ge två stycken råd för dig som tycker att det är svårt med matematik eller att komma igång och plugga matte.

Motivation och den där drömmen

Eftersom jag jobbar halvtid med att undervisa elever på en gymnasieskola i Göteborg så är det förstås ganska vanligt att jag möter även de som inte känner motivation alls för att plugga matte. Ofta så är det kommentarer som ”varför skall man kunna det här?”, ”vilken nytta har jag av det här?” eller ”jag fattar inget av detta” man kan få höra i klassrummet.

Själv så får jag erkänna att jag tycker att det är kul att få ha möjligheten och utmaningen att få ändra på detta synsätt inför matematiken som ämne. Jag brukar utmana mig med att få alla att tycka att matematik är kul (har inte lyckats fullt ut än men skam den som ger sig…).

Men du som läser det här inlägget har troligtvis redan kommit så långt att du vill lyckas med din kurs och göra något åt känslan av att ha svårt för matte. Jag tror att ett bra sätt att komma framåt är att ha ett bra mål med sina studier. Det mesta brukar vara mer överkomligt om man faktiskt vet varför man gör det. Om du exempelvis drömmer om att få bli läkare eller arkitekt så är det precis det du skall måla upp som en inre bild när du sitter kämpande och tränar på algebra.

Att var medveten om den röda tråden i matematik

Svårt med matte och den röda tråden

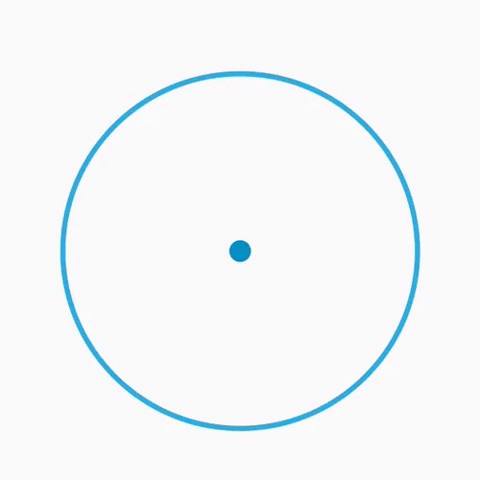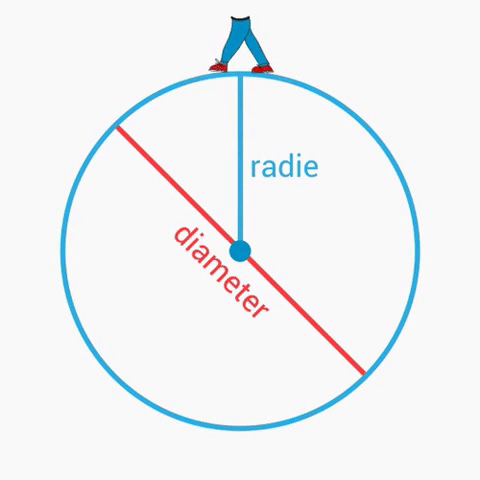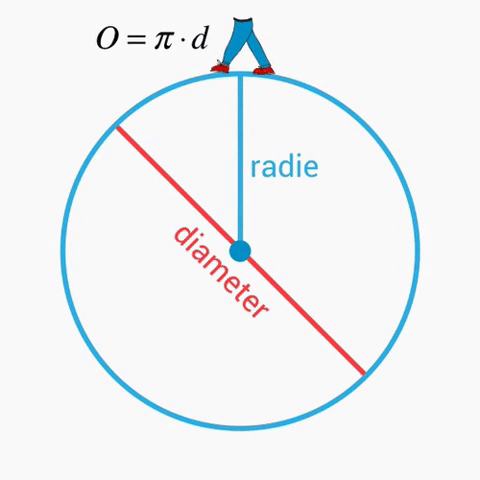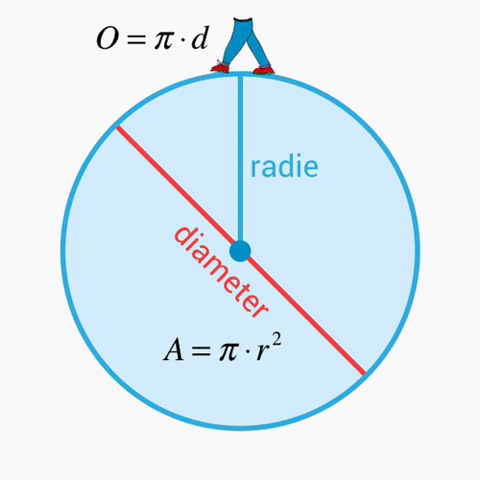
Mycket av det som du pluggar om i mattekurserna hänger ihop som i en röd tråd. För att förstå räta linjens ekvation så är det t.ex. bra att i någorlunda nämnd ordning kunna aritmetik (räkna med tal), algebra, koordinatsystem, grafer och vad en funktion är för något. Det är nämligen ofta så att någon som har svårt för ett speciellt område och att förstå detta har missat något moment tidigare längs den där röda tråden.

Det praktiska tipset här är att skriva ner de begrepp och ord som du inte förstår innebörden av, slå upp dem, och ta reda på vad de betyder. På det viset kommer du enklare att hitta de områden som du kanske har missat och lära dig mer om dem. Det som inte är så bra här är att strunta i att ta tag i dessa områden vilket kan göra att det blir alltmer kunskapsluckor att fylla igen på slutet.

Om du får igång denna vana så kommer det att hjälpa till på vägen att komma igång och komma ur svårigheter i matematiken. I nästa inlägg i den här serien så fortsätter vi med ännu mer konkreta och praktiska tips för dig som har svårt med matten.

Har du ett tips till redan nu eller håller du inte med? Kommentera gärna så diskuterar vi vidare tillsammans!

Mer tips om hjälp från oss

Det kommer mycket kommentarer och frågor kring detta ämne och vi har skrivit en del artiklar och tips om detta så vi tipsar om mer saker att tänka på här:

Publicerad

Erfarenheter av helt digitala prov i matematik

2 Svar

Så fungerar Matematikvideos provverktyg

  • Använd som vanliga prov, kapiteltest eller för att variera egna prov.
  • Stöd för att göra proven helt digitalt.
  • Stödsystem för digital och tidseffektiv rättning.
  • Bedömningsanvisningar på förmågenivå och förklaringar av alla uppgifter.
  • Skapar detaljerade förmågematriser för varje elev.
  • Låst helskärmsläge och hinder från att googla och chatta.
  • Alla provuppgifter innehåller förklaringar och koppling till lektioner (videos, texter, övningar).
  • Användarvänlig formelredigerare för lärare och elever.

Testa provbanken gratis

På Matematikvideo ger vi i vår provbank och provverktyg möjligheten att skriva helt digitala prov i matematik. Jag vill därför dela med mig av mina och andra lärares pedagogiska erfarenheter av digitala prov i matematik.

När jag skriver det här så utgår jag från ett specifikt provtillfälle men hämtar även exempel och erfarenheter från de lärare som använder Matematikvideo vid digitala prov. Jag vill framförallt lyfta fram vilka förutsättningar som krävs för att digitala prov skall fungera och hur eleverna skriver formler digitalt. Jag kommer att diskutera hur vi jobbar med skydd mot fusk och avsluta med vilka fördelar och nackdelar det finns med digitala prov.

Det absolut mest positiva med digitala prov har vid mina och andra lärares prov varit att rättningstiden har minskat markant så hur detta är möjligt kommer jag att fördjupa mig i extra mycket.

Här kan du kika in och se hur vår provbank och provverktyg ser ut. Om du vill få tillgång till prov och uppgifter så kan du ansöka om ett testkonto, det är gratis i 30 dagar.

Förutsättningar och elevernas utrustning

Vid det specifika provet som jag nämner i inledningen så hade alla elever varsin bärbar dator som hjälpmedel och går på ett program med IT-inriktning. Våra erfarenhet från andra skolor som inte har en sådan inriktning är att de allra flesta elever har tillräckligt bra datorkunskaper för digitala prov. Viktigt är förstås att de har tillgång till datorer och internet. I Matematikvideos provsystem så krävs det endast internetuppkoppling när provet sätts igång och när det skall lämnas in.

Provet var på andragradsfunktioner och andragradsekvationer i kursen Matematik 2C och eleverna förbereddes inför det digitala provet genom att göra ett träningsprov i systemet så att de vande sig vid hur det fungerade. I träningsprovet lär de sig att använda sig av formelredigeraren och hur helskärmsläget fungerar (läs mer om det nedan).

Provet var upplagt så att sex av de grundläggande E-C uppgifterna rättades automatiskt av systemet. De resterande sex uppgifterna krävde fullständiga redovisningar. Dessa uppgifter rättades av mig som lärare genom rättningsläget i Matematikvideos provverktyg.

Hur eleverna skrev formler

Ekvationsredigerare

En sak som alltid har varit tidskrävande när jag själv har rättat matteprov är tiden det tar att tolka elevernas uträkningar. Ibland är de minst sagt röriga och svårtolkade och att istället få läsa datorbaserade formler lockar i alla fall mig. Men att få elever att kunna skriva formler på datorn kan vara ett problem då det kräver förståelse för hur man använder en digital formelredigerare.

Så hur skrev eleverna formler?

Matematikvideo har en formelredigerare som bygger på LaTex och som är lättanvänd och intuitiv. Det finns även ett antal snabbvägar till de allra vanligaste symbolerna och formlerna som hjälper eleverna med redovisningar. Vår erfarenhet är att eleverna snabbt lär sig att använda vår formelredigerare.

Skydd mot fusk

Digitala prov i matematik

Det finns en hel del fullt berättigade rädslor kring digitala prov och en av dessa är att eleverna får enklare att fuska med tillgången till datorer och internet. Dessa saker har vi givetvis tänkt på och följande skydd mot fusk har Matematikvideo:

  • Provuppgifterna bör göras i helskärmsläge och om en elev försöker lämna provsidan så ”låses” provet. Detta omöjliggör att man tex googlar efter lösningar eller chattar med en kompis. Om en elevs aktiva prov låses av misstag så kan läraren öppna upp det igen och eleven kan fortsätta där denne är i sitt prov.
  • Frågorna kan slumpas ut så att eleverna får uppgifterna i olika ordning.
  • När eleven skrivit i ett svar så döljs detta svar automatiskt på datorskärmen för att bänkgrannen inte skulle kunna tjuvkika.

Vi rekommenderar  även att eleverna har avskiljare mellan sig. Vissa lärare tycker att det är bra att se elevernas skärmar medan andra vill se elevernas ansikten vilket gör att var läraren placerar sig i klassrummet under provet kan variera. Personligen ser jag helst elevernas ansikten vid provtillfället.

De erfarenheter vi har är att under en normal provsituation så räcker detta skydd bra och att det inte är större, snarare mindre, risk för fusk vid digitala prov. Det krävs fortsatt diskussion om skyddet räcker till vid nationella prov eller större slutprov av summativ karaktär men vid mer formativa provtillfällen under terminen så fungerade det bra. Vi tar gärna emot dina farhågor, tips eller funderingar kring detta.

Fördelar och nackdelar med digitala prov i matematik

En bild på hur rättningsläget ser ut i provverktyget. Formlerna i det stora fältet är redovisningar gjorda av eleverna i klassen.

 

Det finns mycket fördelar med digitala prov men också några fallgropar som kan vara viktigt att vara medveten om. Här sammanfattar jag mina och andra lärares fördelar och nackdelar med digital prov:

  1. Proven går snabbare att rätta
    Vid det provtillfälle som jag nämnt tidigare så tog det mig strax under en timme att rätta alla prov (ca 30 stycken). Där rättades sex av uppgifterna manuellt av mig i systemets rättningsläge och resten rättades automatiskt. Viktigt att nämna är även att provet innehåll förmågor på alla nivåer E-A. Provet innehöll också färdiga bedömningsanvisningar, som alla Matematikvideos prov gör, som följde med på skärmen när jag gick igenom elevernas lösningar.
    Du kan välja att rätta ett prov i taget eller en fråga i taget. Det gör att man inte behöver sitta och bläddra mellan olika papper och du kan exempelvis fokuserat gå igenom en provuppgift för alla elever i klassen. Detta gör att det blir mycket mer effektivt när man slipper byta fokus från en fråga till en annan. Dessutom följer bedömningsanvisningarna med på ett lämpligt ställe på skärmen genom hela rättningsprocessen vilket gör att dessa hela tiden finns snabbt tillgängliga. Det är även enklare att följa elevernas redovisningar när de redovisas digitalt.
  2. Det är lätt att ge feedback till eleverna
    Eftersom att elevernas resultat samlas ihop via systemet är det lätt att se vad de behöver träna vidare på. Uppgifterna innehåller även kopplingar till lektionerna i våra matematikkurser vilket gör att eleverna själva kan söka vidare efter mer kunskap på det område som det har kunskapsluckor på. Det går även snabbt att se vad klassen som helhet behöver träna mer på genom klassammanställningen och därmed ge mer effektiv feedback till hela klassen samtidigt.
  3. Eleverna hade lätt att skriva formler digitalt och redovisa lösningar men det tar längre tid
    Det gick oväntat enkelt för eleverna att skriva formler och redovisa lösningar, där var vi ganska förvånade att det var så smidigt. Däremot så tog det längre tid för eleverna att skriva lösningar. Många av eleverna skriver lösningarna på papper först och fyller sedan i dem på datorn. De känner sig ovana att ”tänka genom datorn” istället för med papper och penna så provet kan ta längre tid än förväntat att utföra. Det är alltså viktigt att man antingen har tillräckligt med tid utsatt till provet eller minskar ner antalet längre uppgifter. Det handlar även om att eleverna i större utsträckning måste vänja sig vid att skriva matematik via datorn. Det är vår övertygelse att ju mer man tränar sig på att skriva matematik på datorn desto lättare blir det också att ”tänka via datorn”.
  4. Eleverna kan bli oroliga av att skriva prov digitalt
    En del av eleverna blir oroliga av att skriva ett digitalt prov då det kan vara nytt för dem. De har i vissa fall mycket höga ambitioner och ovana situationer skapar därför en oro att deras förutsättningar att lyckas skulle minska. Ett annat orosmoment var att de kunde få feedback direkt på de automaträttade uppgifterna vid inlämning av provet. I Matematikvideos system kan läraren välja om eleverna skall få feedback direkt på de automaträttade uppgifterna när de har lämnat in provet. Det gjorde att de ångrade sig och oroade sig redan när de lämnat in provet i salen om de såg att de hade gjort fel. Något som vi rekommenderar är attt det kan vara bra att vänta med automatiserad feedback tills alla elever är klara och har sina prov inlämnade.
  5. Det är lätt att sätta betyg
    En stor fördel med digitala prov är enkelheten och tidsbesparingen vid betygssättning. Provsystemet rättade och betygssatte hälften av uppgifterna automatiskt och resten rättades alltså manuellt vid det specifika provtillfället jag nämnt här ovan. Systemet skapar sedan resultatmatriser automatiskt vilket gör att du som lärare direkt får en överblick av hela klassen och individens resultat när provet är färdigrättat.

Idéer inför framtiden

Vi kommer att fortsätta att göra digitala prov i matematik och fortsätta att testa hur detta görs bäst, enklast och effektivast för elever och lärare. Vi tror att framfarten av digitala prov är ett viktigt pedagogiskt steg för oss som matematiklärare att ta. Det innebär förstås inte att vi så snabbt som möjligt måste börja med detta utan det kräver att både vi och eleverna vänjer oss vid att använda de digitala verktygen i matematik.

Forskning har på senare år lyft fram att en av de starkaste faktorerna är feedback i form av formativ bedömning och för att detta skall vara möjligt med rådande klasstorlekar så krävs bra digitala stöd. Här känner vi att digitala prov som är utformade på rätt sätt har en viktig roll att fylla.

Kommentera gärna om du har några frågor eller om du också har provat att göra digitala prov och berätta om dina erfarenheter kring dessa. Om du vill testa vår provbank och provverktyg så är det gratis och ansökan gör du här.

Med vänlig hälsning
Simon Rybrand

Publicerad

Högskoleprovet 2017 – Kom igång och förbered dig

Kommentera

Ska du skriva högskoleprovet nu i vår 2017 och funderar på hur du bäst och snabbast förbereder dig?

Här hjälper vi dig på vägen och samlar ihop några effektiva tips som förbättrar dina matematikfärdigheter inför provet.

 

Vilka matematikområden är viktigast att plugga på?

I de så kallade kvantitativa delarna (Matematik och statistik) på högskoleprovet så är det framförallt gymnasiets kurs Matematik 1b som utgör grunden.

Personligen brukar jag dock säga att det är rätt bra att även plugga på räta linjens ekvation,  algebran, linjära ekvationssystem från Matematik 2 och i alla fall kika på rationella uttryck från Matematik 3. Alla delar som vi rekommenderar att kunna hittar du förstås i vår Högskoleprovskurs.
Testa en HP lektion direkt

För dig som vill se mer specifika matematikområden att plugga på så kan du kika in i det här blogginlägget med tips om XYZ. Tipsen där gäller även för alla matematikdelar på provet.

Hur tränar man upp sin snabbhet?

För att träna upp sin snabbhet så är det viktigaste att vara trygg med de matematiska grunderna och sedan träna på gamla högskoleprov. Sedan kan du fortsätta och träna ännu mer på gamla högskoleprov och krydda med lite träning på huvudräkningsstrategier och överslagsräkning.

Om du vill dyka ner i sådan tekniker och strategier så har vi skrivit om detta när vi tipsade om DTK delen för ett tag sedan här på bloggen. Där hittar du några riktigt bra tips på det här temat.

Hur är man lugn och metodisk på ett prov?

Ett av de allra viktigaste verktygen för att lyckas på ett prov är att hantera sina känslor kring provet. Många blir naturligtvis nervösa när man skriver ett prov. Potentiellt kan ju högskoleprovet betyda att man kommer in på sin drömutbildning eller inte. Men det finns sätt att hantera sin oro och nervositet!

De allra flesta tycker att kunskaperna känns självklara att träna på inför provet, inte så många pratar om alla de känslor man upplever innan, under och efter provet. Det har visat sig att det fungerar rätt bra att skriva om dessa känslor för att kunna hantera dem.

”By writing down one’s negative thoughts, students may come to realize that the situation is not as bad as they thought or that they are prepared to take it on,” said Beilock, an associate professor of Psychology at the University of Chicago.

”As a result, they worry less during the test.”

Vi har tidigare skrivit om just oro och rädslor kring prov i följande två blogginlägg:

 

För dig som känner så här så rekommenderar vi att du läser igenom detta.

 

Publicerad

Om vår kurs till Fysik 1 – Intervju med Daniel

3 Svar

På Matematikvideo tittar hela tiden på att utöka vårt kursutbud. Senaste kursen som vi släppte var Matematik för högstadiet och nu tänkte vi att det var dags att presentera vårt arbete med kursen Fysik 1 genom att intervjua vår fysiklärare Daniel Johansson som jobbar tillsammans med oss för att göra fysiklektioner. Ännu är vi i början av detta arbete men vi tyckte ändå att det kunde vara intressant att intervjua Daniel där han berättar lite om vem han är och vad han blir inspirerad av och vilka tips han har till dig som pluggar fysik.

Hej Daniel, kan du berätta lite om dig själv och vad du gör just nu?

Hej! Just nu jobbar jag delvis med utveckling av material till fysik 1 kursen här på matematikvideo men har även en deltidstjänst som matematiklärare på en gymnasieskola. På fritiden blir det inte lika mycket fysik och matematik för tillfället utan då blir det mer klättring och handarbete.

Vad blir du inspirerad av?

Jag har lätt att bli inspirerad av andra personer, gärna människor som håller på med intressant matematik och fysik – antingen på fritiden eller i yrket.

Vad gör du här på Matematikvideo?

Det kan faktiskt variera lite. Min huvudsakliga syssla är just nu att arbeta med videomaterial för fysik 1 kursen, men emellanåt skriver jag också uppgifter till matematik kurserna eller diskuterar utvecklings möjligheter med Simon.

Vilken utbildning har du?

Direkt efter gymnasiet valde jag att läsa fysikprogrammet på GU, detta är en 5-årig s.k. naturvetarutbildning. Efter att jag hade läst mina tre första år (dvs kandidatprogrammet) så valde jag dock att ta en paus på ett år och läsa kurser i teoretisk filosofi och logik istället. Sedan fortsatte jag med fysiken och läste ett masterprogram i fysik och astronomi. Eftersom jag nu på senare dagar har halkat in på läraryrket så har jag också börjat läsa kurser som till hösten 2016 kommer att leda till en lärarexamen.

Vad tyckte du om ämnena fysik och matematik på gymnasiet?

Jag visste väldigt tidigt att fysik kan vara väldigt intressant, men jag tyckte att gymnasiekurserna inte riktigt bejakade det. Istället började jag läsa böcker i fysik på fritiden och la tid på gymnasiefysiken först när det behövdes. När det kommer till matematiken så tyckte jag den var mer intressant, redan från årskurs ett på gymnasiet.

Hur upplevde du att det var att gå från att plugga matte/fysik på gymnasiet till att plugga dessa ämnen på högskolan?

På högskolan så krävs det ett större eget ansvar från eleverna. Många lärare har ett material som de ska gå igenom och när de har gjort det så är det färdigt. Det finns inte alltid tid för att reda ut alla missförstånd, utan har man inte förstått allt på lektionen så får man diskutera med sina klasskamrater efteråt.

Om du som lärare skulle ge ett eller flera tips till den som vill lära sig fysik så effektivt som möjligt, vilka skulle det vara?

Mitt tips skulle vara att man ska lyssna på det som man känner att man inte förstår. Att inte förstå något är inte en nackdel, det är en möjlighet att fördjupa sin kunskap genom att läsa på om ämnet. Alla elever har saker i kurser som de tycker känns krångliga, men det är de lever som inte ger sig, utan sätter sig ned och försöker reda ut det krångliga som i slutändan får en helhetsbild av hur saker hänger ihop.

Publicerad

Att härleda exakta trigonometriska värden

4 Svar

Du som läser en kurs på gymnasiet som innehåller trigonometri har säkerligen ett flertal gånger suttit och kikat i formelbladet för att ta reda på exakta trigonometriska värden. De allra flesta av oss är förstås nöjda med att denna information finns i formelbladet men det kan också vara intressant att ta reda på hru man faktiskt kan härleda exakta trigonometriska värden.

 

I det här blogginlägget tänkte jag visa några av dessa härledningar för dig som är intresserad av detta. Det är faktiskt inte särskilt svårt så blir inte avskräckt utan ge det en chans. Dessutom är det mycket bra träning på att förstå geometri, trigonometri och enhetscirkeln.

Exakta värden för vinkeln $45°$

När vi skall ta fram värden för sinus, cosinus och tangens så kan vi utgå från en kvadrat med sidorna 1. Vi drar en diagonal mellan två av hörnen och denna blir då enligt pythagoras sats $\sqrt{2}$ och vinkeln nere vid diagonalen blir $45°$. En bild på detta ser ut på följande vis:

Exakta trigonometriska värden vinkeln 45

Vi kan nu få fram exakta trigonometriska värden för sinus, cosinus och tangens. Dessa är

$ tan(45°)=\frac{\text{motstående katet}}{\text{närliggande katet}} = \frac11=1 $

$ sin(45°)=\frac{\text{motstående katet}}{\text{Hypotenusan}} = \frac{1}{\sqrt{2}}= $ $\frac{1·\sqrt{2}}{\sqrt{2}·\sqrt{2}}=\frac{\sqrt{2}}{2} $
Vi förlänger täljare och nämnare med $ \sqrt{2} $ så att vi får heltalsnämnare.

$ cos(45°)=\frac{\text{motstående katet}}{\text{Hypotenusan}} = \frac{1}{\sqrt{2}}= $ $\frac{1·\sqrt{2}}{\sqrt{2}·\sqrt{2}}=\frac{\sqrt{2}}{2} $
Vi förlänger täljare och nämnare med $ \sqrt{2} $ så att vi får heltalsnämnare.

Exakta värden för vinkeln $60°$ och $30°$

För att få fram exakta trigonometriska värden för $60°$ och $30°$ så använder vi istället en liksidig triangel, dvs en triangel där alla sidor är lika långa och alla vinklar är $60°$. Sidorna i den liksidiga triangeln är alla 1. Vi markerar även ut höjden och vinkeln $30°$ uppe vid toppen på triangeln och att halva längden på bassidan är $0,5$.

Vi kan också beräkna höjden med pythagoras sats så vi får den till $ \sqrt{1^2-(\frac12)^2}=\sqrt{1-\frac14}=\sqrt{\frac34}=\frac{\sqrt{3}}{2} $.

Med en bild ser detta ut på följande vis:

Exakta trigonometriska värden vinklarna 30 och 60

Nu använder vi figuren för att ta fram de exakta trigonometriska värdena.

$tan(30°)=\frac12 \big/ \frac{\sqrt{3}}{2} = \frac{2}{2\sqrt{3}}=\frac{1}{\sqrt{3}}$

$sin(30°)=\frac12 \big/ 1 = \frac{1}{2}$

$cos(30°)=\frac{\sqrt{3}}{2}\big/ 1 = \frac{\sqrt{3}}{2}$

Exakta värden för vinkeln $60°$ blir

$tan(60°)= \frac{\sqrt{3}}{2} \big/ \frac12 = \frac{2\sqrt{3}}{2}=\sqrt{3}$

$sin(60°)=\frac{\sqrt{3}}{2}\big/ 1 = \frac{\sqrt{3}}{2}$

$cos(60°)=\frac{1}{2}\big/ 1 =\frac12$

Exakta värden för vinklarna $0°$, $90°$, $180°$, $270°$ och $360°$

När det gäller vinklarna $0°$, $90°$, $180°$, $270°$ och $360°$ så kan vi utgå från enhetscirkeln för att ta fram dessa värden. På enhetscirkeln gäller att radien är $1$ och att
$sin v = \frac{y}{1} = y$ (y-koordinaten på cirkelns rand)
$cos v = \frac{x}{1} = x$ (x-koordinaten på cirkelns rand)

Tangens för de olika värdena får genom sambandet $ tanv=\frac{sinv}{cosv} $

Med en bild ser detta ut på följande vis.

exakta-trigonometriska-varden-0-90-180-270-360

Alla värden här är alltså

Vinkel $sinv$ $cosv$ $tanv=\frac{sinv}{cosv}$
0° 0 1 0/1 = 0
90° 1 0 1/0 ej definierat!
180° 0 -1 0/-1 = 0
270° -1 0 -1/0 ej definierat!
360° 0 1 0/1 = 0

Exakta värden för vinklarna $120°$, $135°$ och $150°$

Vi kan även använda oss av att vi vet exakta värden för vinklarna $30°$, $45°$ och $60°$ samt det vi vet om enhetscirkeln för att ta fram exakta trigonometriska värden för  $120°$, $135°$ och $150°$. Det vi då använder oss av är att $ 180°-60°=120° $, $ 180°-45°=135° $ och $ 180°-30°=150° $. Vi kan rita ut dessa vinklar på följande vis:

exakta-varden-120-135-150

Det som är viktigt att uppmärksamma i den här bilden är att vinkeln $60°$ är på samma höjd som vinkeln $120°$, dvs den har samma y-värde men x-värdet har bytt tecken till minus. På samma vis är det med vinklarna $45°$ och $135°$ samt vinklarna $30°$ och $150°$.

Alltså kan vi sammanställa de exakta trigonometriska värdena i följande tabell.

Vinkel $sinv$ $cosv$ $tanv=\frac{sinv}{cosv}$
120° $\frac{\sqrt{3}}{2}$ $-\frac12$ $-\sqrt{3}$
135° $\frac{\sqrt{2}}{2} $ $-\frac{\sqrt{2}}{2}$ $-1$
150° $\frac{1}{2}$ $-\frac{\sqrt{3}}{2}$ $-\frac{\sqrt{3}}{3}$

Härleda exakta trigonometriska värden – Sammanfattning i tabell

Nu är vi redo att samla alla dessa exakta trigonometriska värden i en tabell som liknar det du hittar i formelbladet.

Vinkel $sinv$ $cosv$ $tanv=\frac{sinv}{cosv}$
0° 0 1 0
30° $\frac{1}{2}$ $\frac{\sqrt{3}}{2}$ $\frac{1}{\sqrt{3}}$
45° $\frac{\sqrt{2}}{2} $ $\frac{\sqrt{2}}{2} $ 1
60° $\frac{\sqrt{3}}{2}$ $\frac12$ $\sqrt{3}$
90° 1 0 ej def.
120° $\frac{\sqrt{3}}{2}$ $-\frac12$ $-\sqrt{3}$
135° $\frac{\sqrt{2}}{2} $ $-\frac{\sqrt{2}}{2}$ $-1$
150° $\frac{1}{2}$ $-\frac{\sqrt{3}}{2}$ $-\frac{\sqrt{3}}{3}$
180° 0 -1 0
270° -1 0 ej def.
360° 0 1 0

 

Publicerad

5 Matteskämt du samtidigt lär dig något av – del 2

Kommentera

I slutet av våren så skrev vi ett blogginlägg om matteskämt som man samtidigt lär sig något av. Då hade jag egentligen några skämt till på lager men väntade med dessa då det annars kanske hade blivit för mycket av det goda.

Problemet med matematikskämt är ju att de kan bli en aningen torra och att man behöver förklara dem. Och skämt som man ofta behöver förklara varför de är roliga så då är de ju egentligen inte särskilt bra skämt. 😉

Med det sagt så sätter igång med fem stycken skämt som vi dessutom förklarar så att du ska förstå varför dessa är (kan vara) roliga.

Duvan och Möbiusbandet

matteskamt-mobiusVarför gick duvan över Möbiusbandet?
För att komma till samma sida…

Förklaring:

Ett möbiusband är ett band som bara har en sida. För att förstå mera hur ett sådant fungerar så kan du läsa det här blogginlägget.

Statistiken är inte alltid exakt

matteskamt-kaninTre statistiker gick ut för att jaga tillsammans. Efter en stund så får de syn på en kanin. Den första statistikern skjuter på kaninen men missar och skjuter över. Den andra statistiken skjuter nu istället men skjuter under kaninen. Den tredje statistikern utbrister då ”Jaaa! Vi fick den!”.

Förklaring:

Det här skämtet syftar till att statistiken kanske inte är lika exakt som andra områden inom matematiken. För att förstå mer om det här kan du undersöka vad standardavvikelse och normalfördelning är.

Varma hörn

Sonen: Pappa, det är så kallt här!
Pappan: Gå och ställ dig i hörnet.
Sonen: Varför?
Pappan: För att det är 90 ° där.

Förklaring:

Det kan vara lätt att blanda ihop att vinkelmått och enheten för temperatur uttalas på samma sätt dvs grader. I ett hörn är ju även vinkeln rätvinklig. Dvs om denna vinkel är 90 °, dock säger detta förstås ingenting om hur varmt det egentligen är.

Sorgliga historier om linjer

I matematiken finns de tre sorgligaste kärlekshistorierna, dessa tre är:

  1. Den om de två linjerna som bara hade en chans att mötas och sedan var tvungna att skiljas för evigt.
  2. Den om parallella linjer som aldrig var menade att mötas.
  3. Den om asymptoterna som kom närmare och närmare och närmare man aldrig fick vara tillsammans med grafen,

Förklaring:

Här behöver vi förstå en del om olika typer av linjer. Vi tar detta punktvis.

  1. Två stycken räta linjer som har olika lutning kan endast skära varandra en enda gång. För att förstå mer om det här kan du titta på en videogenomgång om linjära ekvationssystem.
  2. Om två stycken linjer istället är parallella så har de samma lutning men olika m-värden. Det här får till följd att de aldrig kommer att skära varandra. Dvs de möts aldrig! Se gärna den här videon om parallella linjer.
  3. En asymptot är en rät linje som grafen till en funktion närmar sig. Man brukar dela upp asymptoter i lodräta, horisontella och sneda asymptoter. Funktionen och funktionens graf kommer alltså aldrig att skära asymptoten. Dvs de bara närmar sig och närmar sig varandra i all evighet 🙂

Osmarta gränsvärden

Ett oändligt antal matematiker går in på en bar. Den första matematikern säger: ”Jag vill ha en öl”. Den andra matematikern säger: ”Jag vill ha en halv öl”. Den tredje matematikern säger: ”Jag vill ha en fjärdedels öl”. Den fjärde matematikern säger: ”Jag vill ha en åttondels öl” och så här fortsätter det. Nu börjar bartendern se nöjd ut och ställer fram endast två öl och säger: ”Ni matematiker borde ju verkligen kunna era gränsvärden”

Förklaring:

Det här skämtet syftar till ett speciellt gränsvärde. Nämligen följande gränsvärde:
$ \frac12+\frac14+\frac18+\frac{1}{16}+…=1 $
Så den första matematikern beställer en öl och då de övriga hela tiden beställer mindre och mindre delar av en öl så inser bartendern att han bara behöver ställa fram 2 öl för att
$ 1 + \frac12+\frac14+\frac18+\frac{1}{16}+…=1+1=2 $.

Om du vill läsa mer om det här gränsvärdet så kan du läsa följande artikel.

Publicerad

Räkna med moms – Så fungerar momsen matematiskt

Kommentera

Just nu jobbar vi med procent här på sajten. Det beror på att vi just nu lägger upp och fyller på med fler onlinelektioner till vår kurs med Högstadiematematik. Det här har förstås inneburit att det har blivit ett och annat exempel där vi jobbar med moms då det är så när kopplat till just procent.

Genom åren har jag fått en hel del frågor på just moms. Att just jag får frågor om detta och hur man räknar ut momsen beror nog på att jag är både matematiklärare och jobbar med företag. Så jag tänkte här göra så att jag reder ut några vanliga frågor om moms ur ett matematiskt perspektiv. Jag tänkte inte att vi skall gå igenom några skattetekniska frågor, det är jag verkligen inte kunnig inom. Hur man räknar på det tror jag däremot att jag kan reda ut några saker kring.

Kort om moms och olika momssatser

Moms, eller mervärdesskatt, är något som vi betalar när vi köper varor eller tjänster. Oftast brukar detta ingå i priset när du köper något och det är inte alltid att man tänker på denna skatt som privatperson då alla priser visas inklusive moms. Så kortfattat kan man säga att det här är en skatt på allt som vi köper eller säljer.

Momsen anges i procent och är 25 %, 12 % eller 6 %. Här är det mycket viktigt att förstå momssatsen anger hur stor andel av priset utan moms som skall beskattas. Vi kan alltså inte få fram summan momsskatt genom att beräkna hur mycket 25 % är av priset inklusive momsen utan vi måste beräkna vad 25 % är av priset exklusive denna skatt.

Från pris utan moms till pris med moms

Vi skall börja med att se hur du kan gå från ett pris utan mervärdesskatten till ett pris med mervärdesskatt. Här nedan tar vi ett exempel på detta där vi använder två olika sätt att beräkna priset inklusive moms.

Exempel 1

Vi tänker oss att vi har en tröja som kostar 220 kr utan (exklusive) moms och momsen är 25 % på denna tröja. Då får vi momsen i kronor genom att beräkna

$ 0,25⋅220 = 55\,kr $

Priset inklusive denna skatt får vi nu genom att summera priset utan moms med momsen

$ 220+55=275\,kr $

Här kan vi även använda oss av förändringsfaktorn $1,25$ för att effektivisera våra beräkningar. Då multiplicerar vi priset exklusive moms med förändringsfaktorn $1,25$ som innebär en ökning av priset med 25 %. Då får vi

$ 220⋅1,25 = 275\,kr $

Från pris med moms till pris utan moms

Om vi istället skall gå från priset med moms till priset utan denna skatt så måste tänka på en mycket viktig sak. Momssatsen (tex 25 %) skall ju beräknas på priset utan moms så vi kan helt enkelt inte bara ta reda på vad 25 % är av priset med moms och dra av det. Faktum är att vi kan dividera priset med moms med 1,25 (om momsen är 25%) eller multiplicera det med 0,8 (om momsen är 25 %) men låt oss först kika lite på hur vi kan komma fram till detta.

Låt säga att priset på en tröja är 275 kr inklusive moms och att momssatsen är 25 %. Vi vet att vi kunde multiplicera priset utan denna skatt med 0,25 för att få hur mycket momsen är i kronor och sedan addera priset (exklusive) för att få priset med moms. Med matematiskt språk kan vi uttrycka detta i en ekvation där vi kallar priset utan moms för $x$.

$ 0,25⋅x+x=275 $

Här kan vi förenkla vänsterledet till

$ 1,25x=275 $

För att nu få $x$ ensamt så kan vi dela med $1,25$ och då får vi att

$x = \frac{275}{1,25}=220\,kr$

Vi har redan nämnt här ovan att vi kunde dividera priset med moms med 1,25 för att få priset utan moms och nu kan vi även förstå varför detta fungerar. Skulle momsen istället vara 12 % så dividerar vi istället priset inklusive moms med 1,12. Faktum är att vi även kan får priset utan moms genom att multiplicera med 0,8. Att dividera med 1,25 är nämligen samma sak som att multiplicera med 0,8 då $ 0,8⋅1,25=1 $

Vi tar ett exempel till på detta.

Priset på en dator är $12600\,kr$ (inkl. moms på 25%). Vad är priset exklusive moms?

Här så kan vi dividera med $ 1,25 $ för att få priset utan moms.

$ \frac{12600}{1,25}=10080\,kr $

Vi kan även multiplicera med 0,8 för att få pris utan moms.

$ 12600⋅0,8=10080\,kr $

Sammanfattning

Pris utan moms till pris med moms

Om du har priset exklusive mervärdesskatt så kan du få priset med moms (25 %) genom att multiplicera med 1,25. Skulle momssatsen istället vara 12 % så multiplicerar du med 1,12 och är den 6 % så multiplicerar du med 1,06.

Pris utan moms till pris med moms

Om du har priset inklusive mervärdesskatt (25 %) så kan du dividera med 1,25 eller multiplicera med 0,8 för att få priset utan moms. Skulle momssatsen istället vara 12 % så dividerar du med 1,12 och är den 6 % så dividerar du med 1,06.

Publicerad

Stämmer det att 0,999… = 1?

1 Svar

Frågan ovan har jag ibland fått från elever i klassrummet och även via mail här via Matematikvideo.se. Ofta så har personen som frågar detta hittat detta påstående på nätet och undrar om det verkligen kan stämma? Det finns ju även anledningar att ibland ifrågasätta information som ”hittas” på nätet, självklart stämmer inte allt men i det här fallet så stämmer det faktiskt!

I det här blogginlägget tänkte jag att vi faktiskt reder ut varför det stämmer.

0,999… och oändligheten

En av orsakerna till att det kan vara lite svårt att få tankarna på rätt plats när det gäller det här påståendet är att det är ganska jobbigt får våra hjärnor att förstå begreppet oändlighet. Det går ju inte att visuellt tänka hur oändligheten möjligtvis kan se ut. Jag klarar i alla fall inte av det 😉

Med de tre punkterna på slutet av 0,999… så menar vi att niorna i decimalutvecklingen fortsätter i all oändlighet. Ju fler nio det är desto närmre kommer vi att vara talet 1 och och när det är oändligt antal nior och det finns ingen skillnad kvar.

Två bevis för att visa att 0,999… = 1

$ x = 0,999… $
$ 10x = 9,999…  $
$ 10x-x = 9,999… – 0,999…  $
$ 9x = 9  $
$ x = 1 $

dvs $ 1 = 0,999…. $

Vi kan även göra beviset på följande vis:

$ \frac13=0,333… $
$ 3⋅\frac13=3⋅0,333… $
$ 1=0,999… $

Tycker du att bevisen här är svåra att förstå? Kommentera gärna så kan vi fortsätta diskussionen om detta lite svårgripbara påstående.

Publicerad

Ny kurs på gång – Matematik för högstadiet

Kommentera

Uppdatering – Matematik Högstadiet klar

Vi är nu klara med vår kurs Matematik Högstadiet där vi går igenom matematiken från År 7, 8 och 9. Kursen innehåller just nu (2016-03-11) 72 lektioner med pedagogiska videogenomgångar, Över 500 övningar och förklarande texter. Alla som har ett konto hos oss (både skolor och privatpersoner) får tillgång till innehållet i kursen.

Just nu håller vi på med att utveckla lektioner som riktar sig till dig som pluggar matematik på Högstadienivå. På Matematikvideo.se har vi idag kurser som riktar sig till dig som pluggar matte på gymnasienivå så det är roligt och spännande att även få göra lektioner till högstadiet. I det här blogginlägget tänkte vi berätta lite om det här arbetet och hur du som användare hos oss kan använda dig även av den här kursen.

 

Årskurs 9 Beta – Nästan klar…

Vi har för tillfället valt att sätta den här kursen i så kallad beta (som den grekiska bokstaven β) men att man som kund och användare hos oss ändå kan komma åt den. Med beta menar man ofta att något inte är riktigt klart men att man gärna vill att användarna kommer igång med det för att se att det är bra nog. Om du direkt vill komma åt kursen så hittar du kurssidan till Högstadiet årskurs 9 här. Alla som är kunder hos oss (både skolor och privatpersoner) kommer åt alla videos och övningar till denna kurs precis som med andra kurser. (Uppdatering – Kursen har döpts om till Matematik Högstadiet)

En del är också gratis för alla besökare så att man kan få en känsla för hur våra videolektioner och övningar fungerar. Exempelvis är några sprillans nya genomgångar om procent helt gratis och vem som helst kan använda sig av dessa för att komma igång och förstå vad procent är, hur man skall förstå procentenheter och begreppen andel, del och helhet.

Använd och tyck till

Självklart är vi väldigt glada om du som använder dig av den här kursen tycker till och önskar vad just du behöver. Vi vill gärna att så många som möjligt skall blir hjälpta i sin matematikstudier och ju mer vi vet om vilka problem just du har desto enklare blir att att fokusera på rätt saker. Så tyck till i kommentarer här eller på andra ställen på sajten så syns vi där!

 

Publicerad

Lär dig matte från animeringar och gif bilder

Kommentera

Här på Matematikvideo gillar vi verkligen när det går att visualisera matematiken. Ofta är det ju så mycket enklare att förstå när även bilder, färger och former hjälper till att förklara.

I det här blogginlägget har vi letat upp bilder och även plockat fram egna animeringar vi har gjort genom åren som hjälper dig att få en lite djupare förståelse för några viktiga matematiska begrepp.

Ibland kan vissa bilder vara på en kursnivå som du själv kanske inte har nått fram till ännu, tveka i så fall inte att ställa frågor i kommentarerna nedan så förklarar vi gärna mera så att du hänger med!

Vad är egentligen π?

Talet π defineras som $ \pi = \frac{\text{Omkrets}}{\text{Diametern}} $ i en cirkel. Nedan visualiseras just detta om diameterna är 1 längdenhet. Då kommer nämligen omkretsen att vara just $\pi$.

Källa: imgur

Vattenbevis av Pythagoras sats

Den här giff-bilden är ett riktigt snyggt sätt att först varför summan av kvadraterna i en rätvinklig triangel är lika med kvadraten av hypotenusan. Om du vill läsa mer om detta rekommenderas det här inlägget om Pythagoras sats eller den här videolektionen.

Pascal

Sierpinskis triangel är ett sätt att färglägga pascals triangel. Man låter här jämna tal få en färg och ojämna tal en annan färg. Då får man den här snygga triangeln. Läs gärna mer om detta i det här blogginlägget.

Se gärna en videolektion om Binomialsatsen och pascals triangel

Volymen för en kon och cylinder

Volymen för en cylinder är $ V = \pi⋅r^2⋅h $ och volymen för en kon är en tredjedel av detta, dvs $ V = \frac{\pi⋅r^2⋅h}{3} $. Här är en kul gif som hjälper dig att komma ihåg detta!

Publicerad