Författare: Fredrik Vislander
Fredrik Vislander

I den här lektionen ska vi titta på något som kallas för svängningsrörelse. Svängningar, eller oscillationer som det också kallas, är inom fysiken en periodisk rörelse som sker kring ett jämviktsläge och mellan två ytterlägen. Sådana rörelser är mycket vanliga i naturen och vardagen. T ex en gunga på en lekplats, armarna när du går, hoppande på en studsmatta och pendelklockor. Till och med atomer vibrerar periodiskt i molekyler. Detta gör att kunskap om hur svängningsrörelser fungerar är viktiga i fysiken. Vi ska särskilt titta på en idealiserad svängningsrörelse som kallas harmonisk svängningsrörelse.
Harmonisk svängningsrörelse
Det finns olika sätt att definiera harmonisk svängningsrörelse, men här räcker det att utgå från att en harmonisk svängningsrörelse är en jämn periodisk rörelse, som sker kring ett jämviktsläge och mellan två ytterlägen. Vi bortser även från friktion, och det innebär att rörelsen inte dämpas utan fortsätter svänga på samma sätt hela tiden. Harmonisk svängningsrörelse kallas ”simple harmonic motion” på engelska och förkortas därför ibland SHM.
Ett första enkelt exempel skulle kunna vara en boll som läggs på kanten i en friktionsfri skål och släpps.
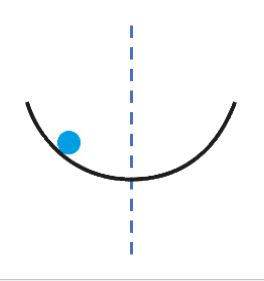
Bollen svänger mellan två ytterlägen och svängningen sker kring ett jämviktsläge i botten på skålen.
Om vi analyserar situationen ur ett energiperspektiv så har bollen i ytterlägena en viss potentiell energi, men ingen kinetisk energi eftersom den ju är stilla i vändlägena.
Den potentiella energin omvandlas under rörelsen mot skålens botten till rörelseenergi och precis i botten, dvs vid jämviktsläget, har all potentiell energi omvandlats till kinetisk energi. Bollen har därför sin högsta fart här.
Bollen passerar jämviktsläget och farten minskar medan bollens potentiella energi ökar igen, fast nu längs med skålens andra sida. Rörelseenergin omvandlas till potentiell energi.
Bollen gör sedan samma rörelse som tidigare men riktad åt andra hållet.
Eftersom vi bortser från friktion kommer rörelsen att fortsätta på samma sätt.
Andra exempel på svängningssystem är t ex en massa på ett snöre som fås att svänga fram och tillbaka, en så kallad pendel. Detta system har uppenbarligen stora likheter med t ex en gunga. Ytterligare ett exempel, och det system vi ska börja studera, är en massa som hänger i en vertikal fjäder.
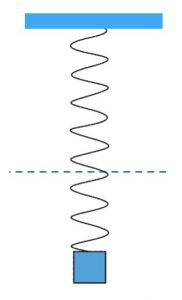
I videon går vi igenom ett antal begrepp och hur de hänger samman med harmonisk svängningsrörelse. Dessa begrepp är viktiga att förstå för att hänga med i resten av kapitlet. Här följer en kort sammanställning av dessa begrepp.
Periodtid
Tiden det tar utföra en ”hel rörelse” eller en hel svängning, dvs att objektet går från ett startläge, utför svängningen, och sedan kommer tillbaka till startläget igen, kallas för svängningstid, periodtid eller bara period och betecknas TT .
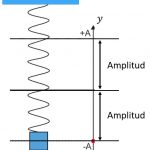
Amplitud
Avståndet mellan jämviktsläget och ett ytterläge kallas amplitud och betecknas AA . Det övre vändläget har yy-koordinaten +A, och det undre vändläget har yy-koordinaten –A. Rörelsen pendlar alltså mellan dessa två lägen. Amplituden är ett positivt värde med SI-enheten meter.
Frekvens
Frekvens definieras som antal svängningar per sekund och betecknas med fƒ . SI-enheten är s11s och denna enhet har fått namnet 11 Hz (Hertz).
Vinkelfrekvens eller vinkelhastighet
En harmonisk svängningsrörelse kan kopplas ihop med cirkelrörelse, och detta leder till begreppet vinkelfrekvens eller vinkelhastighet. Detta är hastigheten som vinkeln ökar med under svängningsrörelse, och betecknas med den grekiska bokstaven ωω . SI-enhet är rad/s.
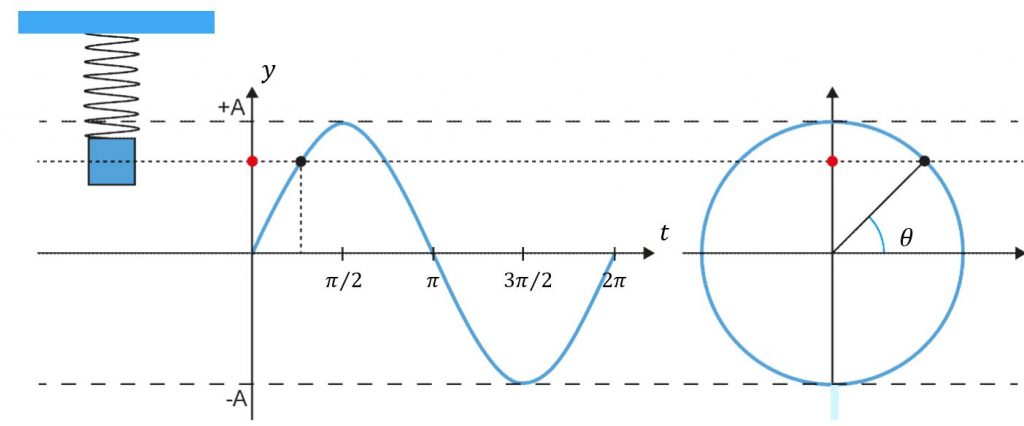
Elongation
Massans position på yy-axeln kallas elongation och betecknas med yy. Elongationen kan också sägas vara massans avvikelse från jämviktsläget. En harmonisk svängningsrörelse kan beskrivas med en sinusfunktion, och detta ger att elongationen kan uttryckas som:
y=Asinθy=Asinθ
Vinkelhastighet definieras som ω=ω= tθθt . Vinkelförändringen för ett helt varv är 2π2π rad, och tiden för ett helt varv är TT . Det innebär att vi även kan ange vinkelhastigheten som ω=ω= T2π2πT . Sedan tidigare vet vi att T=T= f11ƒ .
Genom att använda dessa samband kan vi skriva:
θ=ωtθ=ωt ⇒⇒ y=Asin(ωt)y=Asin(ωt)
eller
ω=ω= T2π2πT =2πf=2πƒ ⇒⇒ y=Asin(2πft)y=Asin(2πƒ t)
Kommentarer
e-uppgifter (4)
1.
(1/0/0)E C A B 1 P PL M R K En massa på en fjäder utför en harmonisk svängningsrörelse. Avståndet mellan ytterlägena är 2222 cm. Vad är rörelsens amplitud? Svara i cm.
Svar:Ditt svar:Rätt svar: 11 cm(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- +1
- Rättad
Rättar...-
2.
(1/0/0)E C A B 1 P PL M R K Lisa är hemma hos sin farmor och farfar. De har ett gammalt pendelur. Lisa mäter tiden det tar pendeln att göra 6060 svängningar till 2,02,0 minuter. Vad är pendelns frekvens?
 Svar:Ditt svar:Rätt svar: 0,50 Hz(Korrekta varianter)Bedömningsanvisningar/Manuell rättning
Svar:Ditt svar:Rätt svar: 0,50 Hz(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- +1
- Rättad
Rättar...-
3.
Du ser en flicka gå över en hängbro. När hon kommer till mitten på hängbron börjar hon hoppa i jämn takt och hela bron utför en harmonisk svängningsrörelse. Du räknar att bron gör 1010 hela svängningar på 6,06,0 sekunder. Beräkna periodtiden.
Svar:Ditt svar:Rätt svar: 0,60 s(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- +1
- Rättad
Rättar...-
4. Premium
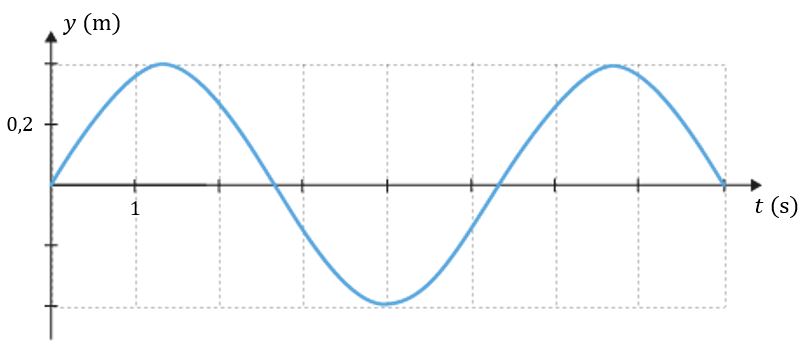
(1/0/0)E C A B 1 P PL M R K En harmonisk svängningsrörelse beskrivs i figuren nedan. Vad är amplituden, frekvensen och perioden?
 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättning- +1
- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
c-uppgifter (1)
5. Premium
(0/1/0)E C A B 1 P PL M R K En harmonisk svängningsrörelse beskrivs av funktionen y=0,005⋅sin(30πt)y=0,005·sin(30πt). Bestäm:
a) amplituden
b) vinkelfrekvensen
c) frekvensen
d) perioden
e) elongationen vid tiden 10,010,0 ms
Bedömningsanvisningar/Manuell rättning- +1
- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Eddler
POPULÄRA KURSER
FÖRETAGSINFO
Eddler AB
info@eddler.se
Org.nr: 559029-8195
Kungsladugårdsgatan 86
414 76 Göteborg

Endast Premium-användare kan kommentera.