Författare: Fredrik Vislander
Fredrik Vislander
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Innehåll

I den här lektionen ska vi titta på ljud och ljudvågor. När vi pratar om ljud menar vi oftast longitudinella vågor i mediet luft, men ljudvågor kan även färdas i andra medier såsom vatten och metall. I den här lektionen kommer vi dock att uteslutande prata om ljudvågor i luft.
Vad är ljud och ljudvågor?
Vi har i tidigare lektioner pratat om stående vågor i strängar, t ex i en gitarrsträng. Men hur kommer det sig att vi uppfattar en våg i en sträng som ett visst ljud?
Det första vi måste påminna oss om är att luft är en gas och att en gas består av många små partiklar. Om en gitarrsträng då befinner sig i gasen luft och vibrerar på ett specifikt sätt, med en specifik frekvens, kommer partiklarna närmast omkring strängen att börja vibrera på samma sätt, med samma frekvens. Strängen blir alltså en vågkälla. Denna störning i luften kommer sedan att fortskrida utåt i alla riktningar och till sist nå trumhinnan i våra öron, som även den kommer börja vibrera med samma frekvens. Örats konstruktion kommer sedan att göra så att vibrationerna omvandlas till nervsignaler, som skickas till hörselcentrum i våra hjärnor. Hjärnan tolkar sedan till sist dessa signaler som det vi kallar ljud.
I videon tittade vi på en animering där membranet hos en högtalare skapade en störning i luften i form av områden med högre tryck och områden med lägre tryck. Dessa förtätningar och förtunningar färdas sedan genom mediet (luften) tills de når exempelvis ett öra. Notera att det inte är någon specifik luftmolekyl som färdas från källan till mottagaren, utan återigen är det själva vågorna, dvs energin, som färdas i mediet. (Situationen då luftmolekylerna själva färdas längre sträckor är det som vi kallar för vind eller blåst, vilket är ett helt annat fenomen.)
Amplituden och perioden hos en longitudinell våg
I animeringen i videon såg vi att en specifik partikel visserligen rör sig, men den oscillerar endast kring ett jämviktsläge när områdena med olika tryck passerar.
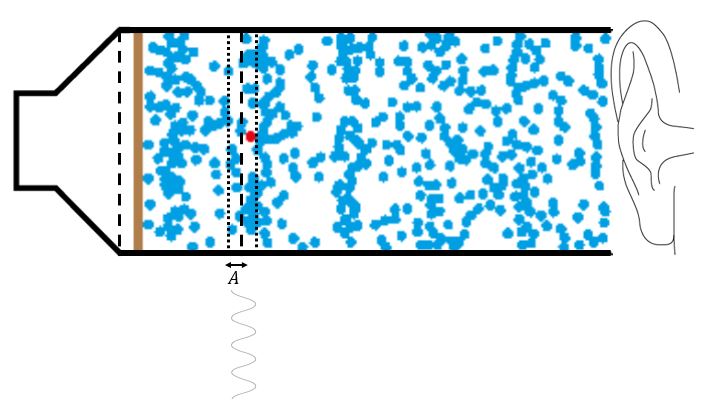
Det maximala avståndet som en enskild partikel rör sig kring detta jämviktsläge tolkar vi som amplituden för en longitudinell våg. Vi kan även definiera perioden som den tid det tar för en enskild partikel att göra en hel oscillation kring jämviktsläget.
Avbilda en longitudinell våg som en transversell våg
Där luftpartiklarna ligger tätare har vi ett lufttryck som är högre än normalt, medan vi vid förtunningarna har ett lufttryck som är lägre än normalt. Det är därför vanligt att avbilda en ljudvåg i en graf med tryck på yy-axeln och position på xx-axeln. Som vi tidigare sagt, kan vi även tolka en enskild partikels maximala avvikelse från sitt jämviktsläge som vågrörelsens amplitud. Som vanligt hos en periodisk våg är våglängden avståndet mellan två på varandra följande förtätningar eller förtunningar. Vi ser att en longitudinell vågrörelse går att avbilda som en transversell vågrörelse, vilket ofta är mer informativt.
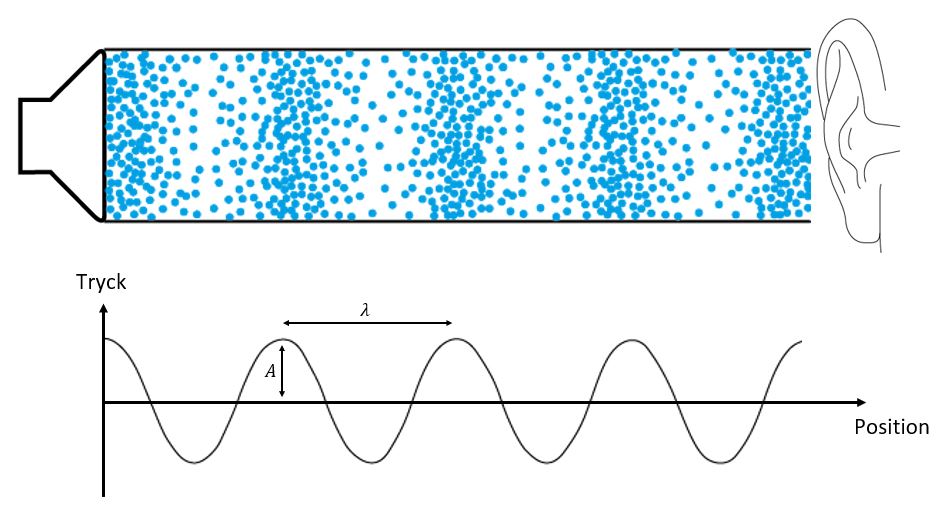
Ljudstyrka och frekvens
Ljudstyrkan, alltså hur starkt vi uppfattar ett ljud, har med oscillationernas storlek att göra, dvs med amplituden. Ett starkare ljud är förknippat med större amplitud. Vi kommer titta mer på detta i nästa lektion.
Ljudets tonhöjd, dvs om vi uppfattar ljudet som ”ljust” eller ”mörkt” beror på frekvensen eller omvänt på våglängden. När det gäller ljud är det dock vanligast att använda frekvensen för att ange tonhöjden. En ton högre upp till höger på en pianoklaviatur låter ”ljusare” och har en högre frekvens än en ton längre ner åt vänster på klaviaturen som ju låter ”mörkare”. Om vi anslår en tangent hårdare eller svagare är det amplituden vi påverkar, inte frekvensen.
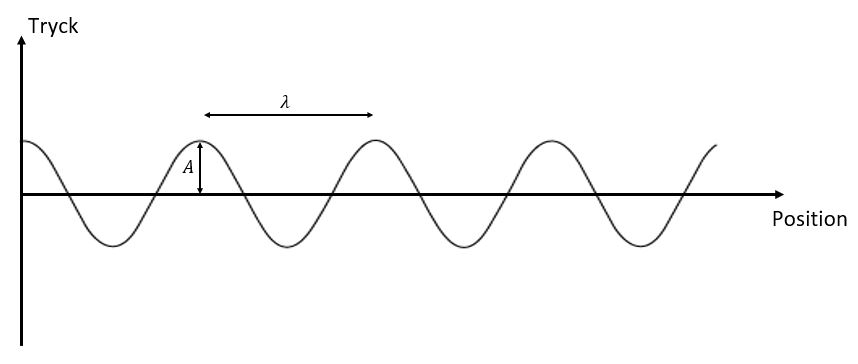 | 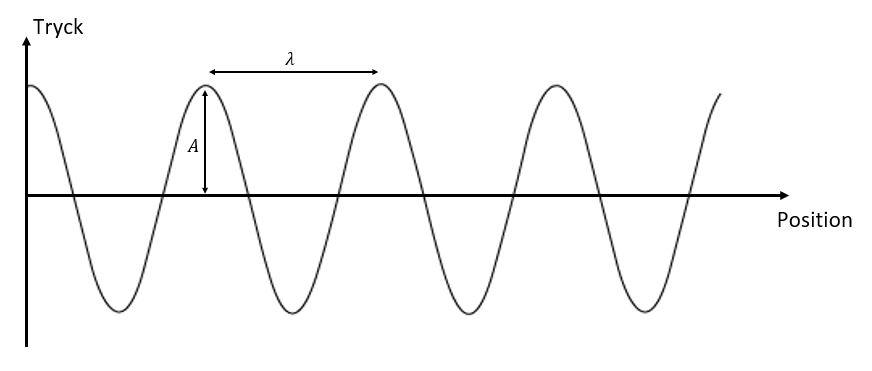 | 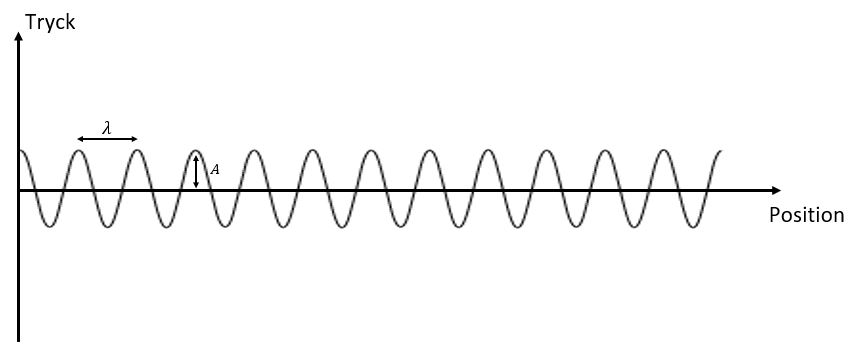 |
I figurerna ser vi först en ljudvåg med en viss amplitud och frekvens från t ex ett piano (bild 1). Om vi trycker ned samma tangent fast hårdare får vi en ljudvåg med samma frekvens men med större amplitud (bild 2). Om vi istället slår an en ton högre upp på klaviaturen och samtidigt anslår svagare blir frekvensen högre och amplituden lägre (bild 3).
Ljudets hastighet
Vi har tidigare pratat om att vågor utbreder sig med en viss bestämd hastighet som beror på mediets egenskaper. Detta gäller även ljudvågor. När ljudvågorna utbreder sig i luft brukar hastigheten anges som 343343 m/s. Ljudhastigheten är dock beroende av flera faktorer, t ex luftens temperatur, luftfuktigheten och luftdensitet, och detta värde gäller vid 20 ∘C20 ∘C och torr luft. I exempel och övningar här kommer 340340 m/s användas för ljudets hastighet i luft (dvs två värdesiffror). Notera återigen att med ljudhastigheten menar vi inte hastigheten hos enskilda luftpartiklar, utan hastigheten som själva störningen, ljudvågorna, färdas med.
Våghastigheten i ett medium beror bland annat på densiteten, och därför är ljudhastigheten högre i vätskor och ännu högre i metaller. Exempelvis är ljudets hastighet i vatten ca 15001500 m/s och ljudhastigheten i stål ca 60006000 m/s. Det känns ju rimligt att det är lättare för partiklarna att knuffa till sina grannar i medier med högre densitet än i lägre, vilket då också ger en högre utbredningshastighet.
Precis som vi nämnt tidigare är våghastigheten konstant v=△t△sv=△s△t , vilket i detta fall kan skrivas som v=Tλ=λfv=λT =λƒ . Detta gäller även för ljudvågor. Du kan alltså inte spela en ton med en högre frekvens och därmed öka våghastigheten. Det som händer när du ökar frekvensen är att våglängden minskar med samma faktor, vilket håller hastigheten konstant. Du kan inte heller öka hastigheten genom att öka volymen, det som händer då är att amplituden ökar. Fundera på hur det skulle låta om du var på en konsert och ljudets hastighet var olika beroende på hur starkt de olika instrumenten spelar. För att ändra ljudhastigheten måste du alltså ändra mediets egenskaper eller byta medium helt och hållet.
Stående vågor i pipor – Halvöppna pipor
Kanske har du spelat på en panflöjt eller något liknande instrument? Varje pipa på en panflöjt består av ett rör som är stängt, ”slutet” i den ena änden, men öppet i den andra. Sådana pipor kallas därför halvöppna (eller ibland slutna) pipor. Du alstrar ljud genom att blåsa i den öppna änden av pipan. Det som händer då är att luften i pipan sätts i svängning vid den öppna änden. Denna svängning fortplantas i luften tills den möter pipans slutna ände där den då reflekteras.
Precis som i strängar kommer de reflekterade vågorna i pipan att interferera med de nya vågor som färdas i pipan åt andra hållet. Beroende på pipans längd kommer vissa frekvenser att bilda stående vågor i luftpelaren i pipan. Det är detta som alstrar tonen som hörs.
Och precis som med stående vågor i strängar kan stående vågor bildas på flera sätt i pipor. I videon tittar vi på flera animeringar som visar hur de stående vågorna bildas i luftpelaren inuti piporna.
Viktigt: I den öppna änden kan luften svänga relativt fritt. Här har vi således en buk. Vid den slutna änden är däremot luften hindrad att vibrera, och här bildas därför en nod. Det blir alltid på detta sätt i pipor. Öppen ände innebär alltid en buk, och sluten ände innebär alltid en nod. Detta kommer att hjälpa oss när vi löser uppgifter.
Vi tittar nu på de enklaste stående vågorna som kan bildas i en halvöppen pipa.
Det är svårt att tydligt illustrera de longitudinella vågorna i luften. Därför ritas stående vågor i pipor som i figuren nedan, men det är viktigt att komma ihåg att detta bara är ett sätt att illustrera den stående vågen. Det som egentligen händer i pipan liknar mer det vi ser i animeringen i videon.
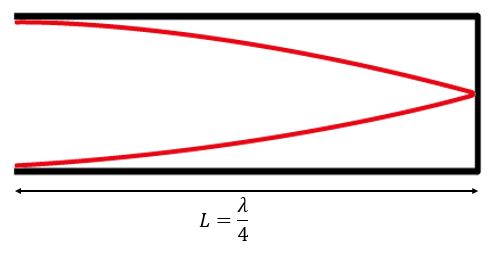
Grundsvängningen, eller grundtonen, får vi när det bildas en buk vid den öppna änden och en nod vid den slutna änden, som vi ser i figuren. Det som figuren egentligen illustrerar är partiklarnas förskjutning från sina jämviktslägen, dvs hur kraftigt de oscillerar på olika platser i pipan.
Om vi kallar pipans längd för LL ser vi att längden i det här fallet motsvarar en fjärdedels våglängd, och vi kan skriva att L=4 λ1L= λ14 . Vi inför återigen ett index nn som motsvarar vilken svängning det handlar om, i detta fall är n=1n=1. Hur tar vi reda på frekvensen? Om vi löser ut våglängden ur sambandet och kombinerar λ1=4Lλ1=4L med v=λ1f1v=λ1ƒ 1 får vi att f1=4Lvƒ 1=v4L .
Nästa stående våg, 1:a övertonen, får vi när det bildas en nod vid den slutna änden och en buk vid den öppna, det måste det ju alltid göra, men nu har den stående vågen ytterligare en nod. Det ger en stående våg med två noder och två bukar enligt figuren. Hur många våglängder motsvarar detta?
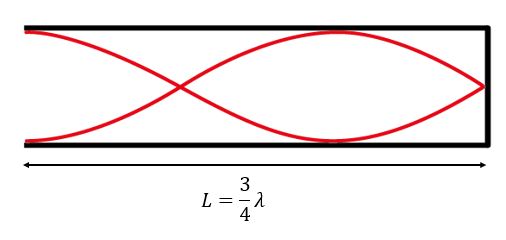
Vi ser i figuren att pipans längd motsvarar 33 fjärdedels våglängder, dvs L=43λ2L=34 λ2 och n=2n=2 . Vi får även att f2=4L3v=3f1ƒ 2=3v4L =3ƒ 1 .
Tittar vi på nästa stående våg, 2:a övertonen, har vi som vanligt en nod vid den slutna änden och en buk vid den öppna, och däremellan 22 noder. pipans längd motsvarar nu 55 fjärdedels våglängder, dvs L=45λ3L=54 λ3 och n=3n=3 . Frekvensen blir f3=4L5v=5f1ƒ 3=5v4L =5ƒ 1 .
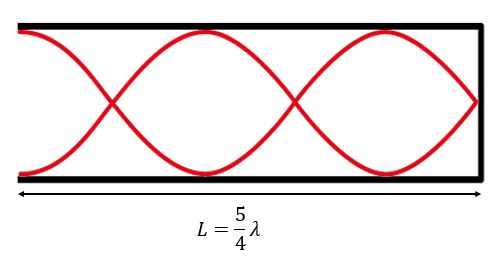
Kan vi urskilja några mönster?
Ja, vi får att L=4(2n−1)λL=(2n−1)λ4 och att fn=4L(2n−1)v=(2n−1)f1ƒ n=(2n−1)v4L =(2n−1)ƒ 1 .
Stående vågor i pipor – (hel)öppna pipor
När det gäller pipor som är öppna i båda ändar uppstår bukar vid båda ändarna. På ett liknande sätt som med halvöppna pipor får vi stående vågor med olika antal noder. I videon går vi igenom de första stående vågorna i helöppna pipor, och resultatet sammanfattas nedan.
Sammanfattning stående vågor i pipor
Halvöppen pipa
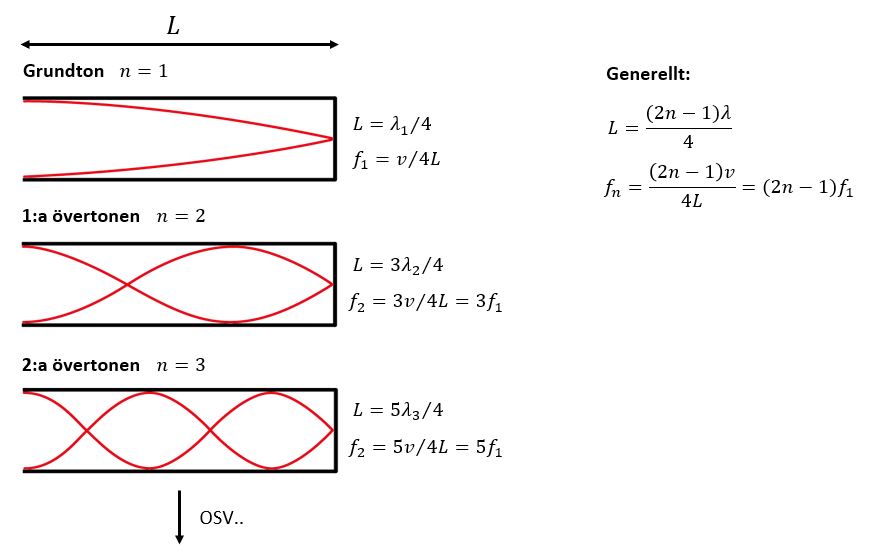
Helöppen pipa
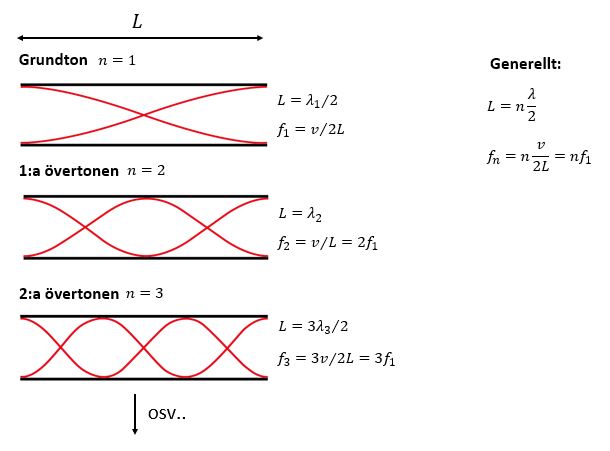
Observera: I alla övningsuppgifter utgår vi från att ljudets hastighet i luft är 340340 m/s.
Exempel
Vilken längd måste en halvöppen pipa ha om vi vill att den ska producera en grundton med frekvensen 440440 Hz?
Lösning
Ett sätt att lösa detta är att titta på hur många fjärdedels våglängder som får plats i pipan då grundtonen genereras. Vi har ju tidigare sett att det för grundtonen är ¼ våglängd.
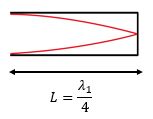
Det innebär att vi kan skriva att L=41λL=14 λ.
Men vilken våglängd handlar det om? Ja, om frekvensen är 440440 Hz kan vi beräkna motsvarande våglängd genom sambandet
v=λfv=λƒ ⇒⇒ λ=fv=440340=0,77…λ=vƒ =340440 =0,77… m.
Vi sätter nu in detta i uttrycket för pipans längd:
L=41λ=41⋅0,77…=0,193…L=14 λ=14 ·0,77…=0,193… m
Svar: Pipan måste vara 1919 cm lång för att generera en grundton på 440440 Hz.
Kommentarer
e-uppgifter (3)
1.
(1/0/0)E C A B P PL 1 M R K Hur lång måste en halvöppen pipa vara för att alstra en grundton med frekvensen 587,3587,3 Hz? Svara i hela cm.
Svar:Ditt svar:Rätt svar: 14 cm(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- +1
- Rättad
Rättar...-
2.
(1/0/0)E C A B P PL 1 M R K En helöppen pipa har en längd på 5050 cm. Vad är grundtonens frekvens?
Svar:Ditt svar:Rätt svar: 340 Hz(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- +1
- Rättad
Rättar...-
3.
(1/0/0)E C A B P PL 1 M R K En halvöppen pipa har en längd på 1,21,2 m. Vad blir våglängden hos 2:a övertonen?
Svar:Ditt svar:Rätt svar: 0,96 m(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- +1
- Rättad
Rättar...-
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
c-uppgifter (2)
4. Premium
(0/1/0)E C A B 1 P PL M R K Är det möjligt att skapa en stående våg med en frekvens på (ca) 212,5212,5 Hz i en helöppen kyrkorgelpipa på 2,42,4 m? Vid vilket nn sker då detta?
Bedömningsanvisningar/Manuell rättning- +1
- Rättad
Rättar...5. Premium
(0/1/0)E C A B P PL 1 M R K En människas örongång kan betraktas som en halvöppen pipa med en längd på 3,03,0 cm. Vad blir våglängden hos den 44:e övertonen som kan bildas i ett sådant rör. Svara i cm med rätt antal värdesiffror.
Svar:Ditt svar:Rätt svar: 1,3 cm(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- +1
- Rättad
Rättar...-
a-uppgifter (1)
6. Premium
(0/0/1)E C A B P PL 1 M R K I en helöppen pipa skapas stående vågor med bl.a. frekvenserna 136136 Hz, 204204 Hz och 272272 Hz. Det skapas inga stående vågor med frekvenser mellan dessa. Vad är frekvensen hos pipans grundton?
Svar:Ditt svar:Rätt svar: 68 Hz(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- +1
- Rättad
Rättar...-
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Eddler
POPULÄRA KURSER
FÖRETAGSINFO
Eddler AB
info@eddler.se
Org.nr: 559029-8195
Kungsladugårdsgatan 86
414 76 Göteborg

Elias Henebrink
det står avrunda till hela cm, svaret 343/587.3 blir 0,584…/4 blir 14.6cm alltså 15cm
Sara Petrén Olauson
Hej! Det stämmer om vi anger ljudets hastighet som v=343 m/s (vilket brukar användes vid 20∘C och torr luft). Ljudhastigheten beror dock av flera faktorer, såsom luftens temperatur, luftfuktigheten och luftdensitet. Vill vi ha ett bredare värde kan vi istället använda två värdesiffror, vilket ger v=340 m/s. Det är detta värde som används i alla exempel och övningsuppgifter här. Hoppas att det blev tydligare nu.
Matteo Krans Dusic
I förklaringen används värdet v = 340 m/s, men den anges aldrig i själva frågan.
Sara Petrén Olauson
Hej! Ljudhastigheten i luft beror av flera faktorer, såsom luftens temperatur, luftfuktigheten och luftdensitet. I exempel och övningar här används v=340 m/s för ljudets hastighet i luft (dvs två värdesiffror). Hoppas att det var svar på din fråga och hjälper dig att komma vidare.
Raimas Hazaea
hur får du till v blir 340 i sista frågan i videon?
Sara Petrén Olauson
Hej! v=340 m/s är ljudets hastighet i luft. Ljudhastigheten beror av flera faktorer, såsom luftens temperatur, luftfuktigheten och luftdensitet. Vid 20∘C och torr luft bukar v=343 m/s användas. Vill vi ha ett bredare värde kan vi istället använda två värdesiffror, vilket ger v=340 m/s. Det är detta värde som används i alla övningsuppgifter här.
Hoppas att det blev tydligare nu!
Endast Premium-användare kan kommentera.