
Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Matematik 1c
/ Centrala Begrepp Matematik 1
Sammanfattning Matematik 1c
Innehåll
- Fyra prioriteringsregler
- Negativa tal
- Rationella tal – Bråk
- Inverser
- Talmängder
- Tal på olika former
- Potenser
- Grundpotensform
- Algebra – Att lösa Ekvationer
- Förenkla algebraiska uttryck
- Multiplicera och Faktorisera uttryck
- Linjär olikhet
- Funktioner
- Tre olika sätt att beskriva funktionen
- Definitionsmängd och Värdemängd
- Räta linjens ekvation i k-form
- Proportionalitet
- Parallella linjer
- Vinkelräta linjer
- Räta linjens ekvation i allmänform
- Förändringsfaktor
- Amortering och Ränta
- Exponentialfunktion
- Exponentialekvation
- Potensfunktion
- Potensekvationer
- Prefix
- Geometri
- Pythagoras sats
- Triangel
- Parallellogram
- Parallelltrapets
- Cirkel
- Cirkelsektor
- Prisma
- Pyramid
- Kon
- Klot (Sfär)
- Cylinder
- Kub
- Vinklar
- Trianglar
- Trigonometri
- Vektorer
- Skala
- Statistik
- Felmarginal
- Lägesmått
- Spridningsmått
- Sannolikhet
- Problemlösning, verktyg och tillämpningar
- Repetitionsmaterial
- Kommentarer
![]() I sammanfattning Matematik 1c har vi samlat alla formler och begrepp som du behöver i kursen Matematik 1c. Du hittar lätt vad du söker i innehållsförteckningen här till höger.
I sammanfattning Matematik 1c har vi samlat alla formler och begrepp som du behöver i kursen Matematik 1c. Du hittar lätt vad du söker i innehållsförteckningen här till höger.
Sammanfattning Matematik 1c är främst till för att ge dig en överblick över kursen. Den är till hjälp vid repetition inför prov. Genom att klicka på länkarna i texten kommer du till lektioner med övningsuppgifter och videogenomgångar på de olika begreppen. På så sätt kan du fördjupa dig mer kring det som här, i all enkelhet, kort presenteras. Följ länken för att se hur skolverket beskriver kursens centrala innehåll.
För att se vår fullständiga kurs gå till Matematik 1c.
En annan bra repetition av kursen är att göra nationella prov som gjort tidigare år. Vi har samlat dem på ett ställe.
Vill du träna fler uppgifter på en särskild betygsnivå eller ett centralt innehållsområde så använd vår uppgiftsgenerator.
Fyra prioriteringsregler
När du beräknar värdet av ett uttryck eller löser ekvationer behöver du ta hänsyn till prioriteringsreglerna och använda dem i rätt ordning. Här presenteras de i fallande styrka.
- Innehåll i parenteser
- Potenser (”upphöjt till” och ”roten ur”)
- Multiplikation och Division
- Addition och Subtraktion
Negativa tal
Ett minustecknet är ett tecken för räkneoperationen subtraktion, för att beteckna negativa tal och/eller för att beteckna motsatt tal.

Här har vi samlat reglerna för beräkningar med de fyra räknesätten och negativa tal. För de positiva talen $a$a och $b$b gäller att
Addition av negativa tal
$a+\left(-b\right)=a-b$a+(−b)=a−b Olika tecken i följd ersätts med en subtraktion (-).
Subtraktion av negativa tal
$a-\left(-b\right)=a+b$a−(−b)=a+b Två lika tecken i följd ersätts med en addition (+).
Multiplikation av negativa tal
$a\cdot\left(-b\right)=-a\cdot b$a·(−b)=−a·b
$\left(-a\right)\cdot b=-a\cdot b$(−a)·b=−a·b En positiv och en negativ faktor ger en negativ produkt.
$\left(-a\right)\cdot\left(-b\right)=a\cdot b$(−a)·(−b)=a·b Lika tecken på faktorerna ger en positiv produkt.
Division av negativa tal
$\frac{a}{-b}=\frac{-a}{\text{ }b}=-\frac{a}{b}$a−b =−a b =−ab Olika tecken på täljare och nämnare ger en negativ kvot.
$\frac{-a}{-b}=\frac{a}{b}$−a−b =ab Lika tecken på täljare och nämnare ger en positiv kvot.
Rationella tal – Bråk
De rationella talen kallas även för bråk. De består av en täljare och en nämnare.
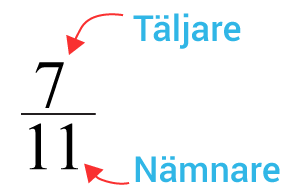
Bråktal skrivs antingen i bråkform eller i blandad form.
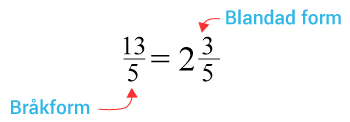
När du förlänger eller förkortar ett bråktal, så innebär det att du multiplicerar eller dividerar både täljaren och nämnaren med samma tal. Följande räkneregler gäller för de rationella talen.
Addition
$\frac{a}{b}+\frac{c}{d}=\frac{a}{b}\cdot\frac{d}{d}+\frac{c}{d}\cdot\frac{b}{b}=\frac{ad+bc}{bd}$ab +cd =ab ·dd +cd ·bb =ad+bcbd
Subtraktion
$\frac{a}{b}-\frac{c}{d}=\frac{a}{b}\cdot\frac{d}{d}-\frac{c}{d}\cdot\frac{b}{b}=\frac{ad-bc}{bd}$ab −cd =ab ·dd −cd ·bb =ad−bcbd
Multiplikation
$\frac{a}{b}\cdot\frac{c}{d}=\frac{ac}{bd}$ab ·cd =acbd
Division
$\frac{\frac{a}{b}}{\frac{c}{d}}$ab cd $=\frac{a}{b}$=ab $\big/$ $\frac{c}{d}=\frac{a\cdot d}{b\cdot c}$cd =a·db·c
Inverser
Två tal vars produkt är lika med ett är varandras inverser.
Exempelvis är $\frac{a}{b}$ab och $\frac{b}{a}$ba varandras inverser eftersom att $\frac{a}{b}\cdot\frac{b}{a}=$ab ·ba =$1$1
Talmängder
I lektionen Tal och talsystem går vi igenom de olika talmängderna mer ingående, men här repeterar vi dem kort.
Naturligt tal
Alla heltal större eller lika med noll.
$\mathbf{N}=$ { $ 0, \, 1,\, 2,\, 3, \, 4, \, 5, \, …$}
Heltal
Mängden av alla naturliga och negativa heltal.
$ \mathbf{Z}=$ { $ …-2,\, -1,\, 0, \, 1, \, 2…$}
Rationellt tal
Mängden av alla tal som kan skrivas som en kvot av två heltal $a$ och $b$, där $b≠0$.
$ \mathbf{Q}=$ { alla tal $\frac{a}{b}$ab , där $a$ och $b$ är hela tal och $b≠0$}
Irrationellt tal
Reella tal som inte är rationella.
Reella tal
Varje punkt på en kontinuerlig tallinje motsvarar ett reellt tal.
$ \mathbf{R}=$ { alla tal på tal linjen}
Tal på olika former
I kursen Matematik 1 behöver du kunna omvandla tal mellan följande olika former.
Decimalform
Tal skrivna på en form, med siffror på båda sidor om ett decimaltecknet är skrivna på decimalform.
Bråkform
Tal skrivna på formen $\frac{a}{b}$ab , där täljaren $a$ och nämnaren $b$ är hela tal och $b≠0$ är bråktal. Även kallade rationella tal.
Procentform
Tal skrivna på formen $a\%$a% är skrivna på procentform.
Potenser

Tal skrivna på formen $a^x$ax, där $a$a är en bas och $x$x en exponent kallas potenser. Skrivsättet motsvarar att basen $a$a multipliceras med sig själv $x$x gånger.
Potensregler
För alla reella tal $m$m och $n$n och positiva tal $a$a och $b$b gäller att
$a^m\cdot a^n=a^{m+n}$am·an=am+n
$\frac{a^m}{a^n}$aman $=a^{m-n}$=am−n
$a^{-n}=$a−n= $\frac{1}{a^n}$1an där $a\ne0$a≠0
$(a^m)^n=a^{m\cdot n}$(am)n=am·n
$\left(\frac{a}{b}\right)^n=\frac{a^n}{b^n}$(ab )n=anbn
$(a\cdot b)^n=a^n\cdot b^n$(a·b)n=an·bn
$a^{\frac{1}{n}}=\sqrt[n]{a}$a1n =n√a
$a^0=1$a0=1
Grundpotensform
Tal skrivna på formen $ a \cdot 10^b $ där $ 1≤ a <10 $ och $b$ är ett heltal är skrivna på grundpotensform.
Algebra – Att lösa Ekvationer
En ekvation är en likhet mellan två uttryck, där åtminstone ett av dem är algebraiskt.

I en ekvation kalls det okända i uttrycket för en variabel. Ofta betecknar man denna med ett $x$.
Målet när man löser en ekvation är att hitta de värden som gör att vänsterledet är lika med högerledet. Lösningen till ekvationen kallas även för en rot.
Man kan lösa en ekvation på många olika vis. En del är effektivare än andra. Här är en metod.
Ekvationslösning
- Förenkla uttrycken i höger och vänsterledet.
- Samla alla variabeltermer i ena ledet, genom att subtrahera med den minsta variabeltermen på båda sidor om likhetstecknet.
- Samla alla konstanttermer i ena ledet, genom att addera det motsatta talet till den minsta konstanttermen på båda sidor om likhetstecknet.
- Multiplicera eller dividera båda leden så att variabelns koefficient blir en etta.
Denna metod fungerar inte alltid, men kan vara en bra ram att utgå från.
Du kan alltid kontrollera att du fått rätt lösning genom att ersätta variabeln i den ursprungliga ekvationen med din rot. En korrekt lösning ger alltid att vänsterledet antar samma värde som högerledet, eller med andra ord, $VL=HL.$VL=HL.
Ekvationer med nämnare löser du lättast genom att först multiplicera alla termer med nämnaren, innan du börjar förenkla de två leden.
Om variabeln inte har exponenten $1$1, upphöjer du båda leden till exponentens invers, alternativ drar roten ur, för att få variabeln med grad ett. Se potensekvationer lite längre fram i texten.
Förenkla algebraiska uttryck
För att göra matematiken effektiv och tydlig vill vi kunna förenkla algebraiska uttryck. Om flera termer i ett algebraiskt uttryck är av samma sort, alltså både variabeln och exponenten är samma, så kan vi addera alternativt subtrahera dessa med varandra, så att vi minskar antalet termer i uttrycket.

Multiplicera och Faktorisera uttryck
När vi utvecklar uttryck med parenteser, även kallat multiplicera in, ska alla termer i parentesen multipliceras med faktorn.

När vi faktoriserar ett algebraiskt uttryck så skriver vi om en summa till en produkt. Att faktorisera är motsatsen till att multiplicera in, som vi gör när vi utvecklar uttryck.
Genom att först uppmärksamma de faktorer som finns i alla termer, kan vi sedan ”bryta ut” dem från termerna och skriva som en faktor framför parentesen.

Kvar inne i parentesen blir det som ”är kvar” i varje term efter att du brutit ut gemensamma faktorer. Viktigt att komma ihåg när du bryter ut hela termens värde är att det ändå finns en etta kvar i parentesen.
Linjär olikhet
En linjär olikhet uttrycker en storleksrelation mellan olika matematiska uttryck av första graden.
När vi dividerar eller multiplicerar med ett negativt tal byter olikheten riktning. Annars löser man olikheter precis som andra ekvationer.
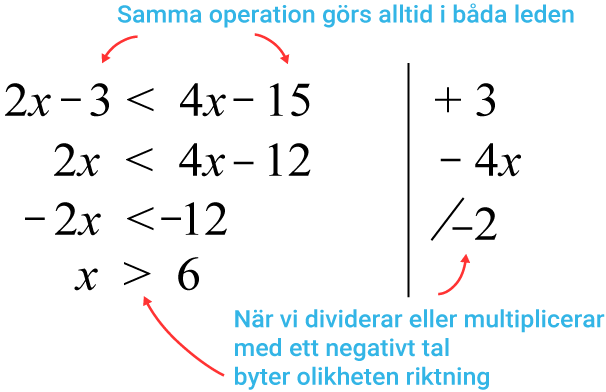
Man kan skriva de tal som finns i ett viss intervall, eller mängd, som en olikhet.
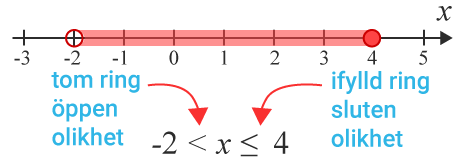
Funktioner
En funktion beskriver ett samband mellan två eller flera olika saker och man använder ofta variabeln $x$x och variabeln $y$y för att beskriva detta samband. I Matematik 1 är det fokus på att veta skillnaden mellan linjära och exponentiella funktioner.
Tre olika sätt att beskriva funktionen
Vi beskriver funktionen med en ekvation eller formel, med en värdetabell och med en graf.
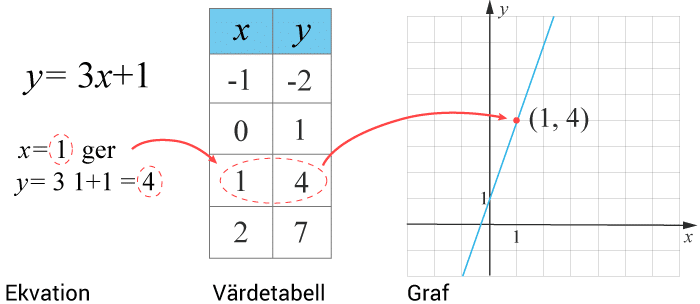
Du behöver kunna sambanden och röra dig mellan dessa tre olika beskrivningar av funktionen.
Genom att sätta in olika $x$x -värden i ekvationen kan du beräkna de tillhörande funktionsvärden $y=f\left(x\right)$y=ƒ (x). Med talparen, $x$x och $y$y, kan du skapa en värdetabell. Talparen motsvarar koordinater till punkter på grafen. Alla punkters koordinater uppfyller likheten i funktionens ekvation.
Definitionsmängd och Värdemängd
Begreppet definitionsmängd motsvarar alla värden som för funktionen är tillåtna för den oberoende variabel, ofta $x$x. Eller med andra ord, de $x$x-värden som är förutbestämda på något sätt eller gör det möjligt att beräkna ett tillhörande funktionsvärde.
Begreppet värdemängd motsvarar alla värden som blir givna, eller erhålls, utifrån funktionsuttrycket och den oberoende variabel. Värdemängden motsvarar alltså funktionsvärdena och betecknas ofta med variabeln $y$y. Eller med andra ord, värdemängden är de $y$y -värden som tillhör funktionen utifrån definitionsmängden.
Vilka $x$x-värden som är tillåtna varierar från funktion till funktion.
Ett exempel skulle kunna vara att man i grundläggande geometriska sammanhang bara ”tillåter” $x$x-värden som är större än noll. Det beror på att vi sällan pratar om längder, areor eller volymer som är negativa.
Räta linjens ekvation i k-form
En förstagradsfunktion kallas även för en linjär funktion och dess graf är en rak linje, en så kallad rät linje. Den kan beskrivas matematiskt med likheten y = kx + m där bokstäverna i formeln betyder följande.
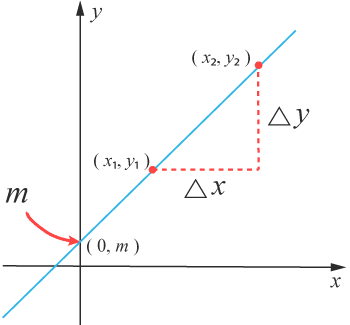
- k är en konstant som motsvarar linjens lutning. Konstanten kallas även riktningskoefficienten.
- m är en konstant som motsvarar -värdet där linjen skär -axeln.
- $x$x och $y$y variablerna i funktionen som ger alla punkter $\left(x,\text{ }y\right)$(x, y) på grafen.
Värdet på konstanten $k$k, som alltså motsvarar linjens lutning, kan bestämmas med hjälp av två valfria punkter på linjen. $\bigtriangleup y$△y motsvarar förändringen i $y$y -led och $\bigtriangleup x$△x förändringen i $x$x -led mellan de två punkterna.
$k=$k= $\frac{\bigtriangleup y}{\bigtriangleup x}=\frac{y_2-y_1}{x_2-x_1}$△y△x =y2−y1x2−x1
I denna kurs ska du kunna bestämma det räta linjens ekvation samt ange en mängd olika egenskaper linjen har.
Positiv lutning – $y$y-värdet ökar när $x$x-värde ökar. I räta linjens ekvation är $k>0$k>0.
Negativ lutning – $y$y-värdet minskar när $x$x-värde ökar. I räta linjens ekvation är $k<0$k<0.
Lutning lika med noll – $y$y-värdet blir oförändrat när $x$x-värde ökar. I räta linjens ekvation är $k=0$k=0 .
Saknar lutning – grafen motsvarar en lodrät linje och ingen funktion. En sådan linjens ekvation är $x=a$x=a där $a$a motsvarar värdet där grafen skär $x$x -axeln.
Alla punkter $\left(x,\text{ }y\right)$(x, y) som ger att likheten $y=kx+m$y=kx+m stämmer ligger på linjen.
Proportionalitet
Då $m=0$m=0 får vi funktionen $y=kx$y=kx. Grafen till funktion går då alltid genom origo.
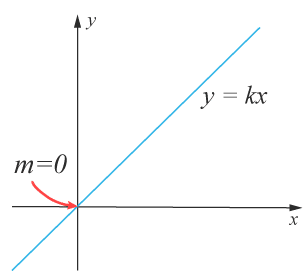
En funktion på denna form kallas för proportionell och man säger att $y$y är proportionellt mot $x$x. Konstanten $k$k kallas då i stället för proportionalitetskonstanten.
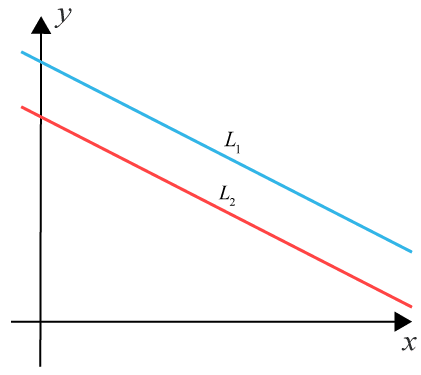
Parallella linjer
Två linjer $L_1=k_1x+m_1$L1=k1x+m1 och $L_2=k_2x+m_2$L2=k2x+m2 är parallella då de har samma lutning.
Alltså då $k_1=k_2$k1=k2
Vinkelräta linjer
Två linjer $L_1=k_1x+m_1$L1=k1x+m1 och $L_2=k_2x+m_2$L2=k2x+m2 är vinkelräta då de har en vinkel mellan dem som är $90^{\circ}$90∘.
Detta gäller då $k_1\cdot k_2=-1$k1·k2=−1
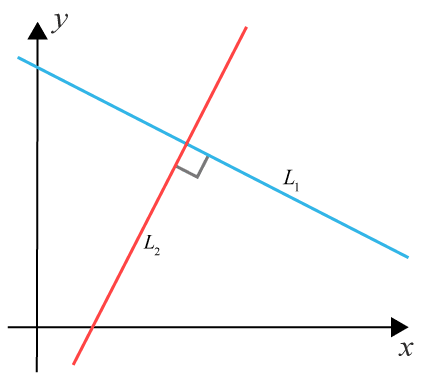
Som följa av detta kan du därmed undersöka om linjer är parallella eller vinkelräta genom att jämföra linjernas $k$k -värden.
Räta linjens ekvation i allmänform
$ax+by+c=0$ax+by+c=0 , där inte både $a$a och $b$b är noll
Förändringsfaktor
När man jobbar med procentuell förändring kommer användandet av förändringsfaktorn väl till pass. Du beräknar den med följande kvot.
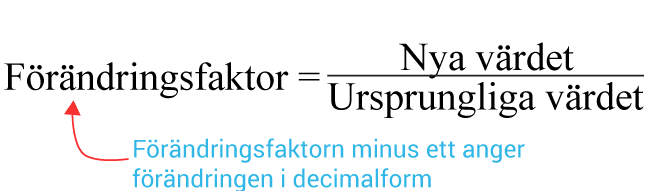
Vid upprepade procentuella förändringar får du den totala förändringsfaktor genom att multiplicera alla förändringsfaktorer med varandra.
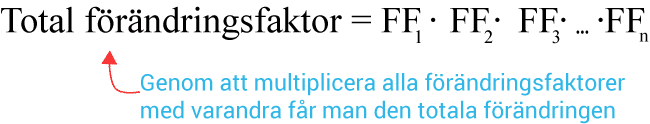
Förändringsfaktorn $a<1$a<1 motsvarar en minskning.
Förändringsfaktorn $a>1$a>1 motsvarar en ökning.
Förändringsfaktorn $a=1$a=1 motsvarar ett oförändrat resultat.
Amortering och Ränta
Utöver ovanstående behöver du kunna använda av kalkylprogram för beräkning av ränta och amortering.
Exponentialfunktion
En funktion där variabeln återfinns i exponenten är en exponentialfunktion. Den skrivs på formen $y=C\cdot a^x$y=C·ax där $C$C och $a$a är konstanter och $a>0$a>0.
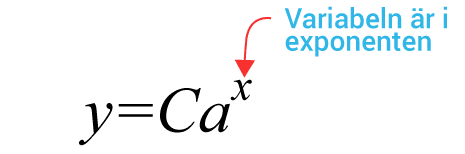
$y$y motsvarar funktionsvärdet
$C$C motsvarar startvärdet, funktionens värde när $x=0$x=0
$a$a motsvarar förändringsfaktorn
$x$x motsvarar ofta antalet förändringar
Exponentialfunktioner är effektiva att använda då man har procentuella förändringar som upprepas sig.
Växande då $C$C är positivt och $a>1$a>1. Förändringsfaktorn motsvarar en procentuell ökning.
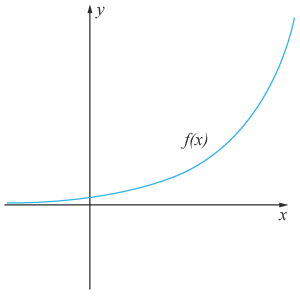
Avtagande då $C$C är positivt och $0<$0< $a<1$a<1. Förändringsfaktorn motsvarar en procentuell minskning.
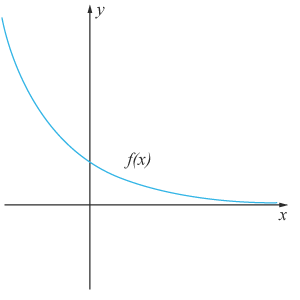
Om $C$C är ett negativa tal kommer grafen speglas i $x$x -axeln. Du kan med fördel undersöka exponentialfunktionens utseende genom att skriva in olika värden på $C$C och $a$a i ett digitalt hjälpmedel.
Exponentialekvation
I Matematik 1c använder vi grafisk lösning när vi löser exponentialekvationer. Skriv om ekvationen så att du endast har en konstant i ena ledet. Lösningen till ekvationen motsvarar då $x$x-värdet i den punkt som har ett $y$y-värde som motsvarar konstanten.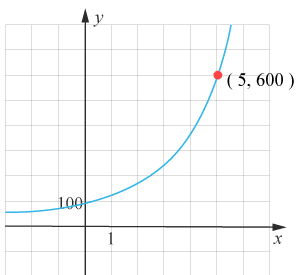
Ovan visas grafen till funktionen $y=100\cdot1,43^x$y=100·1,43x . Vi hittar lösningen till ekvationen $600=100\cdot1,43^x$600=100·1,43x i punkten $\left(5,\text{ }600\right)$(5, 600) då $HL=600$HL=600 när $x=5$x=5 vilket därmed motsvarar lösningen till ekvationen.
Med hjälp av ett digitalt hjälpmedel finner vi lösningen genom att skriva in VL och HL som två olika funktioner och använder därefter grafräknarens funktion för att bestämma deras skärningspunkt. Ekvationens lösning motsvaras av skärningspunktens $x$x -värdet.
Potensfunktion
En funktion där variabeln återfinns i basen kallas för en potensfunktion. Den skrivs på formen $y=k\cdot x^n$y=k·xn där $k$k och $n$n är konstanter.
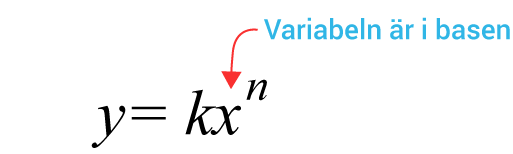
Potensekvationer
En potensekvation är en ekvation där variabeln återfinns i basen. Genom att skriva om ekvationen, så att variabeltermen är ensam i ena leden och har koefficienten ett, kan man sedan lösa ekvationen med roten ur eller upphöja båda leden med exponentens inverterade värde.
Sammanfattningsvis gäller att
$\sqrt[n]{a^n}=a$n√an=a och $\left(a^n\right)^{\frac{1}{n}}$(an)1n $=a$=a
vilket leder till att
$a^{\frac{1}{n}}=\sqrt[n]{a}$a1n =n√a
Om ekvationen har en jämn exponent, finns det två reella lösningar till ekvationen – en negativ och en positiv lösning.
Om ekvationen har en udda exponent, finns det bara en reell lösning.
Prefix
Prefix används till att beskriva stora och små tal med hjälp av bokstäver. Du får tillgång till denna tabell på formelsamlingen vid Nationella proven.
| Symbol | Prefix | Namn | Tiopotens | Decimaltal |
|---|---|---|---|---|
| Y | yotta | Kvadriljon | $10^{24}$ | $1\text{ }000\text{ }000\text{ }000\text{ }000\text{ }000\text{ }000\text{ }000\text{ }000$1 000 000 000 000 000 000 000 000 |
| Z | zetta | Triljard | $10^{21}$ | $1\text{ }000\text{ }000\text{ }000\text{ }000\text{ }000\text{ }000\text{ }000$1 000 000 000 000 000 000 000 |
| E | exa | Triljon | $10^{18}$ | $1\text{ }000\text{ }000\text{ }000\text{ }000\text{ }000\text{ }000$1 000 000 000 000 000 000 |
| P | peta | Biljard | $10^{15}$ | $1\text{ }000\text{ }000\text{ }000\text{ }000\text{ }000$1 000 000 000 000 000 |
| T | tera | Biljon | $10^{12}$ | $1\text{ }000\text{ }000\text{ }000\text{ }000$1 000 000 000 000 |
| G | giga | Miljard | $10^9$ | $1\text{ }000\text{ }000\text{ }000$1 000 000 000 |
| M | mega | Miljon | $10^6$ | $1\text{ }000\text{ }000$1 000 000 |
| k | kilo | Tusen | $10^3$ | $1\text{ }000\text{ }$1 000 |
| h | hekto | Hundra | $10^2$ | $100$100 |
| da | deka | Tio | $10^1$ | $10$10 |
| Ett | $10^0$ | $1$1 | ||
| d | deci | Tiondel | $10^{-1}$ | $0,\text{ }1$0, 1 |
| c | centi | Hundradel | $10^{-2}$ | $0,\text{ }01$0, 01 |
| m | milli | Tusendel | $10^{-3}$ | $0,\text{ }001$0, 001 |
| μ | mikro | Miljondel | $10^{-6}$ | $0,\text{ }000\text{ }001$0, 000 001 |
| n | nano | Miljarddel | $10^{-9}$ | $0,\text{ }000\text{ }000\text{ }001$0, 000 000 001 |
| p | piko | Biljondel | $10^{-12}$ | $0,\text{ }000\text{ }000\text{ }001$0, 000 000 001 |
| f | femto | Biljarddel | $10^{-15}$ | $0,\text{ }000\text{ }000\text{ }000\text{ }001$0, 000 000 000 001 |
| a | atto | Triljondel | $10^{-18}$ | $0,\text{ }000\text{ }000\text{ }000\text{ }000\text{ }001$0, 000 000 000 000 001 |
| z | zepto | Triljarddel | $10^{-21}$ | $0,\text{ }000\text{ }000\text{ }000\text{ }000\text{ }000\text{ }001$0, 000 000 000 000 000 001 |
| y | yokto | Kvadriljondel | $10^{-24}$ | $0,\text{ }000\text{ }000\text{ }000\text{ }000\text{ }000\text{ }000\text{ }001$0, 000 000 000 000 000 000 001 |
Geometri
Den gren av matematiken där man studerar vilka egenskaper figurer i rummet har. Nedan följer en samling av olika kroppar och geometriska figurer.
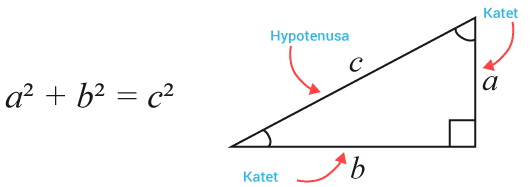
Pythagoras sats
I en rätvinklig triangel gäller att den ena kateten i kvadrat adderat med den andra kateten i kvadrat är lika med hypotenusan i kvadrat.
Triangel
I en triangel är alltid höjden $h$h vinkelrät mot basen $b$b .
$\text{Area}$Area $=\frac{b\cdot h}{2}$=b·h2 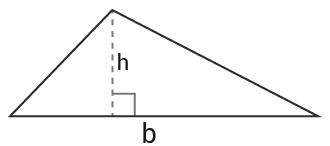
Parallellogram
I ett parallellogram är sidorna parvis lika långa och parallella och höjden $h$h är alltid vinkelrät mot basen $b$b .
$Area=b\cdot h$Area=b·h 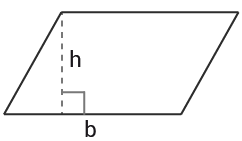
Parallelltrapets
I en parallelltrampets är två sidor parallella och höjden $h$h är alltid vinkelrät mot basen $b$b .
$Area=$Area= $\frac{h\left(a+b\right)}{2}$h(a+b)2 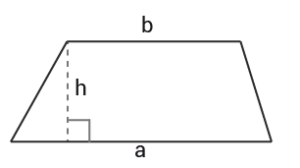
Cirkel
I en cirkel är alltid diametern dubbelt så lång som radien.
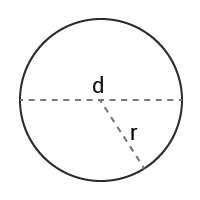
$Omkrets=\pi\cdot d=\pi\cdot2r$Omkrets=π·d=π·2r
$Area=\pi\cdot r^2=$Area=π·r2= $\frac{\pi\cdot d^2}{4}$π·d24
Cirkelsektor
En cirkelsektor motsvarar en del av en cirkel.
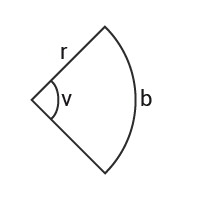
$B\text{å}gen\text{ }\text{ }b=$Bågen b= $\frac{v}{360^{\circ}}$v360∘ $\cdot2\pi r$·2πr
$Area=$Area= $\frac{v}{360^{\circ}}$v360∘ $\cdot\pi r^2$·πr2 $=\frac{br}{2}$=br2
Prisma
Ett prisma är en geometrisk kropp med två baser i form av polygoner. Den ena basen är en parallellförskjutning av den andra och sidoytorna är därför parallellogram. Prismats höjd är det vinkelräta avståndet mellan baserna.
Volymen av ett prisma är arean av basen multiplicerat med höjden.
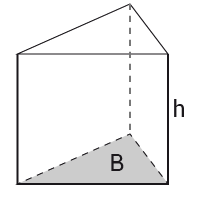
$Volym=B\cdot h$Volym=B·h där $B$B är basytans area.
Pyramid
En pyramid är en geometrisk kropp med en bas i form av en månghörning. Pyramiden bestäms av basen och en punkt, pyramidens spets, som inte ligger i samma plan som basen. Det vinkelräta avståndet mellan basen och spetsen motsvarar pyramidens höjd $h$h.
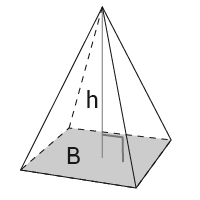
$Volym=$Volym=$\frac{Bh}{3}$Bh3
Kon
En rak cirkulär kon är en geometrisk kropp som bildas av linjer mellan samtliga punkter på konturen av en cirkel och en punkt utanför planet. Det vinkelräta avståndet mellan basen och spetsen motsvarar konens höjd $h$h. Konens sidlängd $s$s kan beräknas med hjälp av $s=\sqrt{r^2+h^2}$s=√r2+h2 där $r$r motsvarar cirkelns radie.
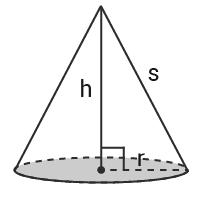
$Volym=$Volym= $\frac{\pi r^2h}{3}$πr2h3
$Mantelarea=\pi rs$Mantelarea=πrs
Klot (Sfär)
Ett klot är en geometrisk solid kropp. Klotets begränsningsyta kallas för en sfär.
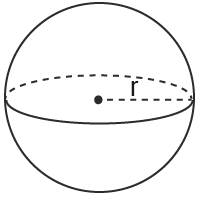
$Volym=$Volym= $\frac{4\pi r^3}{3}$4πr33
$Area=4\pi r^2$Area=4πr2
Cylinder
En cylinder är en geometrisk kropp som avgränsas av två likformiga parallellförskjutna cirklar. Det vinkelräta avståndet mellan ytorna kallas cylinderns höjd $h$h.
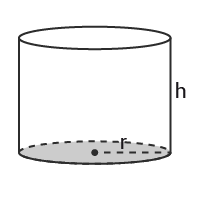
$Volym=\pi r^2h$Volym=πr2h
$Mantelarea=2\pi rh$Mantelarea=2πrh
Kub
I en kub är alla sidor lika långa.
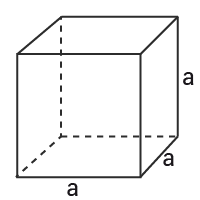
$Volym=a\cdot a\cdot a=a^3$Volym=a·a·a=a3
$Mantelarea=6\cdot a^2$Mantelarea=6·a2
Vinklar
I skärningspunkten mellan två räta linjer uppstår vinklar.
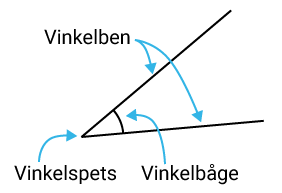
Dessa vinklar har en mängd olika namn.
Spetsiga vinklar
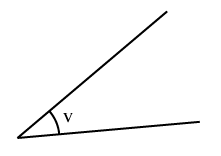 Om en vinkel är mindre än $90^{\circ}$90∘ så kallas den för spetsig. En sådan vinkel $v$v är befinner sig i ett storleksintervall 0° < v < 90°.
Om en vinkel är mindre än $90^{\circ}$90∘ så kallas den för spetsig. En sådan vinkel $v$v är befinner sig i ett storleksintervall 0° < v < 90°.
Räta vinklar
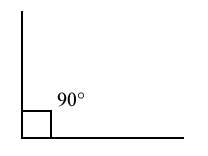 En rät vinkel är lika med $90^{\circ}$90∘ och en sådan vinkel betecknas med raka streck.
En rät vinkel är lika med $90^{\circ}$90∘ och en sådan vinkel betecknas med raka streck.
Trubbiga vinklar
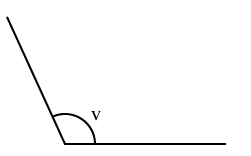 En trubbig vinkel är större än $90^{\circ}$90∘ men mindre än $180^{\circ}$180∘ (rak vinkel). En sådan vinkel $v$v är befinner sig i ett storleksintervall 90° < v < 180°.
En trubbig vinkel är större än $90^{\circ}$90∘ men mindre än $180^{\circ}$180∘ (rak vinkel). En sådan vinkel $v$v är befinner sig i ett storleksintervall 90° < v < 180°.
Raka vinklar
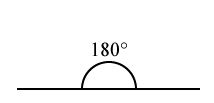 En rak vinkel är lika med $180^{\circ}$180∘.
En rak vinkel är lika med $180^{\circ}$180∘.
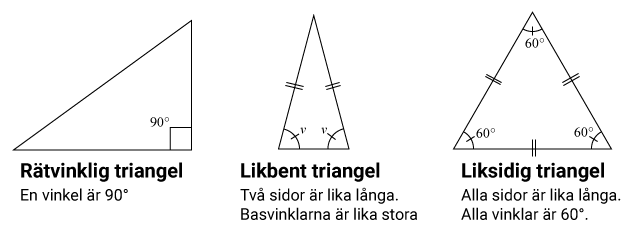
Trianglar
Vinkelsumman i en triangel är alltid $180^{\circ}$180∘ .
Trigonometri
I rätvinklig triangel kan förhållandet mellan vinkeln, katetrarna och hypotenusan beskrivas med följande samband.
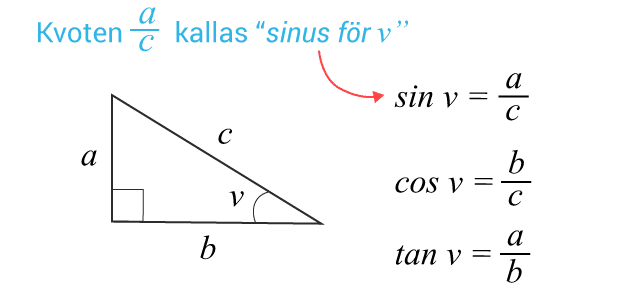
Du behöver kunna bestämma triangelns sidor samt beräkna vinklar med de trigonometriska sambanden ovan. Du bestämmer vinkeln $v$v med de inversa funktionerna $\sin^{-1}\left(\frac{a}{c}\right),\text{ }\cos^{-1}\left(\frac{b}{c}\right)$sin−1(ac ), cos−1(bc ) och $\tan^{-1}\left(\frac{a}{b}\right)$tan−1(ab ).
Vektorer
En vektor är en storhet som både har en storlek och en riktning.
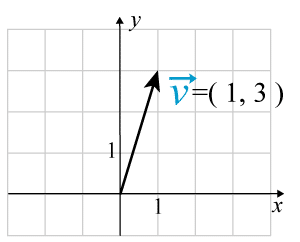
Koordinatform
En vektor som har sin startpunkt i origo kan anges i koordinatform genom att ange ändpunktens koordinater.
Skalär
En skalär beskrivs som en storhet som endast har en storlek.
- Om vektorn $\vec{v}$ multipliceras med skalären $k\ne1$k≠1 så får vi en ny vektor $k·\vec{v}$ som är $k$ gånger så lång som $\vec{v}$. I koordinatform får vi att $k\cdot\vec{v}=k\left(x_v,\text{ }y_v\right)=\left(kx_v,\text{ }ky_v\right)$k·→v=k(xv, yv)=(kxv, kyv)
- Om $k<0$, dvs om $k$ är ett negativt tal, så får vi en ny vektor med motsatt riktning.
Parallellförflyttning
Vektorer kan parallellförflyttas. Det innebära att vektorn kan förflyttas fritt i koordinatsystemet utan att förlora sitt värde, så länge den inte förändras i längd och riktning.
Vektorlängd
Längden på en vektor $ \vec{v}=(a,b) $ beräknas genom
$ |\vec{v}|=\sqrt{a^2+b^2} $
Komposanter och resultant
Om $ \vec{r} = \vec{u}+\vec{v} $ så kallas $\vec{r}$ resultant och $\vec{u},\, \vec{v} $ för komposanter.
Motsatt vektor
Till vektorn $ \vec{v}$ finns en motsatt vektor $ \vec{-v}$
Addition och subtraktion av vektorer
Du bestämmer en summa av vektorer grafiskt, med hjälp av polygonmetoden. Metoden går ut på att vektorerna läggs efter varandra. Första vektors ändpunkt blir nästa vektors startpunkt osv. Summan motsvarar vektorn mellan första vektorns startpunkt till sista vektorns ändpunkt.
Bilden nedan visar $ \vec{u}+\vec{v}=\vec{r} $
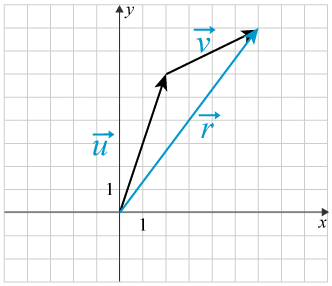
Algebraiskt beräknas vektorer på följande vis.
Vektoraddition
$ \vec{v_1}+\vec{v_2} = (x_1,y_1)+(x_2,y_2)=(x_1+x_2, y_1+y_2) $
Vektorsubtraktion
$ \vec{v_1}-\vec{v_2} = (x_1,y_1)-(x_2,y_2)=(x_1-x_2, y_1-y_2) $
När en vektor subtraheras med en annan vektor så görs egentligen en addition av den motsatta vektorn. Detta då
$ \vec{u}-\vec{v}=\vec{u}+ (-\vec{v}) $ och $(-\vec{v})$ är den motsatta vektorn till $\vec{v}$.
Skala
Med hjälp av skalfaktorn för längdskalan kan vi bestämma även area och volymskalan.
$\text{Areaskala =(Längdskala)}^2$Areaskala =(Längdskala)2
$\text{Volymskala =(Längdskala)}^3$Volymskala =(Längdskala)3
Statistik
I matematik 1c introducerar vi ett antal nya begrepp i statistiken och lär oss granska och värdera statistik material med hjälp av dessa.
Population
Hela mängden individer, objekt eller element som ingår i undersökningen.
Urval
Den metod man använder för att plocka ut stickprovet. Det finns flera olika sätt att göra urval på. Bland annat slumpmässiga urval. Du kan då välja på att antingen göra obundet slumpmässigt urval eller stratifierat urval.
Obundet slumpmässigt urval
Alla individer, enheter eller element i populationen har samma sannolikhet att hamna i stickprovsundersökningen.
Stratifierat urval
Urvalet görs så att alla delgrupper finns representerade i samma proportioner som i den hela populationen.
Stickprovsundersökning
Undersökning på en del av populationen.
Totalundersökning
Undersökning på en hel population.
Frekvens
Antal observationer för ett visst observationsvärde.
Relativ frekvens
Frekvens angiven som andel. Ofta i procent.
Felkällor
Olika saker som kan påverka så att resultatet blir missvisande (fel) vid en statistisk undersökning. Exempelvis bortfall och mätfel.
Bortfall
Den del av urvalet eller populationen som inte ger något resultat. Till exempel inte svarar på en undersökning.
Felmarginal
Med hjälp av följande formel försöker man säkerställa att en undersökning är tillförlitlig.
$f=1,96\cdot$ƒ =1,96· $\sqrt{\frac{p\left(100-p\right)}{n}}$√p(100−p)n
där $n$n är stickprovets storlek och $p$p den procentuella andelen av populationen.
Om ett resultat av en undersökning landar i intervallet för felmarginalen anses undersökningen vara statistiskt säkerställd.
Lägesmått
Lägesmått är värden som sammanfattar alla mätvärden i en datamängd med ett enda representativt värde. I matematik 1 behöver du kunna beräkna och bestämma lägesmåtten medelvärde, median och typvärde både utifrån tabeller och datamängder.
Statistik redovisas ofta i diagramform. Återvänd till lektionen om Vad är statistik för att se de vanligt förekommande diagrammen. Här följer olika lägesmått och begrepp som ingår att kunna i kursen.
Medelvärde
$\text{Medelvärdet}=$Medelvärdet= $\frac{\text{Summan av alla observationsvärden}}{\text{Antal observationer}}$Summan av alla observationsvärdenAntal observationer
Median
Mittenvärdet i datamängden när den står i storleksordning. Vid jämnt antal värden blir medianvärdet medelvärdet av de två mittersta värdena.
Typvärde
Typvärdet är det vanligast förekommande observationsvärdet i en datamängd.
Spridningsmått
Spridningsmått anger hur observationerna i datamängden varierar kring lägesmåttens värden. I matematik 2b och 2c ska du kunna beräkna och bestämma spridningsmåtten variationsbredd, kvartilavstånd och percentiler samt känna till hur man kan beräkna standardavvikelser och jobba med normalfördelat material.
Sannolikhet

Begreppet gynnsamma utfall innebär detsamma som ”alla önskade resultat”, vilket är det vi vill beräkna sannolikheten för.
Begreppet möjliga utfall innebär detsamma som ”alla möjliga resultat”, vilket är alla olika resultat som kan komma att inträffa vid slumpförsöket som vi ska beräkna sannolikheten för.
Multiplikationsprincipen
Om sannolikheten för ett första val är och följande val är så är sannolikheten för att de bägge sker i följd . Självklart kan detta utökas till fler antalet val i följd.
Komplementhändelse
Om $A^c$Ac är komplementhändelse till händelse $A$A gäller att $P\left(A\right)+P\left(A^c\right)=1$P(A)+P(Ac)=1
Träddiagram
Träddiagram används för att beräkna sannolikheter i flera steg där flera vägar är möjliga. Multiplikationsprincipen säger att sannolikheten längs en gren i träddiagrammet ges av produkten av sannolikheterna längs grenen.
Problemlösning, verktyg och tillämpningar
I kursen igår att kunna använda digitala verktyg för att effektivisera beräkningar och komplettera metoder, till exempel vid ekvationslösning.
Dessutom ingår färdigheter i problemlösning som omfattar att upptäcka och uttrycka generella samband, samt som omfattar begrepp och metoder i kursen, med särskild utgångspunkt i karaktärsämnen, privatekonomi och samhällsliv.
Dessa färdigheter kan du öva i våra problemlösnings och tillämpningslektioner.
Repetitionsmaterial
Tyvärr kommer du inte att få tillgång till all information som delas här, i sammanfattning Matematik 1c, vid Nationella provet. Följ länken för att se den Formelsamling du får använda vid Nationella provet Matematik 1c.
Du kan även med fördel använda dig av några av våra kapiteltest. Samtliga uppgifter har fullständiga förklaringar.
Kapiteltest – Aritmetik Ma1c
Kapiteltest – Algebra Ma1c
Kapiteltest – Repetition Procent Ma1c
Kapiteltest – Funktioner Ma1c
Kapiteltest – Trigonometri och Vektorer Ma1c
Kapiteltest – Sannolikhetslära Ma1c
Kapiteltest – Statistik Ma 1c
Centrala begrepp Ma1 Del 1
Centrala begrepp Ma1 Del2
Vill du träna fler uppgifter på en särskild betygsnivå eller ett centralt innehållsområde så använd vår uppgiftsgenerator.
Här kan du hitta alla gamla nationella prov att öva på.


Endast Premium-användare kan kommentera.