
Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Matematik 2
/ Centrala Begrepp Matematik 2
Sammanfattning Matematik 2
Innehåll
- Utveckla och multiplicera parenteser
- Kvadreringsreglerna
- Konjugatregeln
- Faktorisering
- Potensekvationer
- Fem sätt att lösa andragradsekvationer på
- Kvadratrotsmetoden
- Nollproduktmetoden
- PQ-formeln/Lösningsformeln
- Andragradsekvationer på allmänform
- Grafisk lösning
- Rotekvationer och falska rötter (Ma2c)
- Logaritmer
- Räta linjens ekvation i k-form
- Parallella linjer
- Vinkelräta linjer
- Räta linjens ekvation i allmänform
- Linjära ekvationssystem
- Polynom
- Andragradsfunktioner
- Vertex
- Parabelns största och minsta värde
- Nollställen
- Symmetrilinjens ekvation
- Potensfunktioner
- Exponentialfunktioner
- Skala (Ma2c)
- Likformighet
- Kongruens (Ma2b,c)
- Topptriangel- och transversalsatsen
- Bisektrissatsen
- Vinklar
- Kordastasten
- Randvinkelsatsen
- Pythagoras sats
- Trigonometri (Ma2a)
- Avståndsformeln
- Mittpunktsformeln
- Statistik (Ma2b,c)
- Felmarginal
- Lägesmått
- Spridningsmått
- Standardavvikelse för stickprov
- Normalfördelning
- Lådagram
- Repetitionsmaterial
- Kommentarer
![]() I sammanfattning Matematik 2 har vi samlat alla formler och begrepp som du behöver i kurserna Matematik 2a, Matematik 2b och Matematik 2c. Du hittar lätt vad du söker i innehållsförteckningen här till höger.
I sammanfattning Matematik 2 har vi samlat alla formler och begrepp som du behöver i kurserna Matematik 2a, Matematik 2b och Matematik 2c. Du hittar lätt vad du söker i innehållsförteckningen här till höger.
Sammanfattning Matematik 2 är främst till för att ge dig en överblick över kursen. Den är till hjälp vid repetition inför prov eller inför att du ska läsa Matematik 3b eller 3c.
Genom att klicka på länkarna i texten kommer du till lektioner med övningsuppgifter och videogenomgångar på de olika begreppen. På så sätt kan du fördjupa dig mer kring det som här, i all enkelhet, kort presenteras. Följ länken för att se hur skolverket beskriver kursens centrala innehåll.
En annan bra repetition av kursen är att göra nationella prov som gjort tidigare år. Vi har samlat dem på ett ställe.
Vill du träna fler uppgifter på en särskild betygsnivå eller ett centralt innehållsområde så använd vår uppgiftsgenerator.
Algebra
Utveckla och multiplicera parenteser
Vid all räkning med tal och algebraiska uttryck gäller prioriteringsreglerna. Därför gäller att när du multiplicerar en term med en parentes ska alla termer i parentesen multipliceras med faktorn framför parentesen. Regeln kallas för den distributiva lagen och säger att
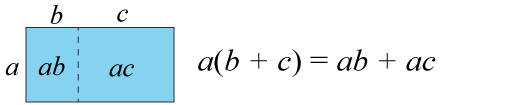
När du multiplicerar parenteser med varandra ska alla termer i parenteserna multipliceras med varandra. Regeln kallas för den utvidgade distributiva lagen och säger att
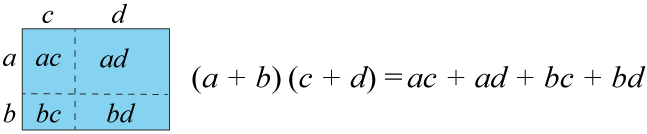
Som följd av detta gäller att två parenteser som är identiska ger de välkända reglerna konjugatregeln och kvadreringsreglerna.
Kvadreringsreglerna
$(a+b)^2=a^2+2ab+b^2$(a+b)2=a2+2ab+b2
$(a-b)^2=a^2-2ab+b^2$(a−b)2=a2−2ab+b2
Konjugatregeln
$(a+b)(a-b)=a^2-b^2$(a+b)(a−b)=a2−b2
Faktorisering
Eftersom att en likhet gäller åt båda håll använder vi ovanstående regler när vi ska faktorisera.
När vi faktoriserar ett algebraiskt uttryck så skriver vi om en summa till en produkt. Att faktorisera är alltså motsatsen till att multiplicera in som vi gör när vi utvecklar uttryck.
Genom att först uppmärksamma de faktorer som finns i alla termer, kan vi sedan ”bryta ut” dem från termerna och skriva som en faktor framför parentesen.
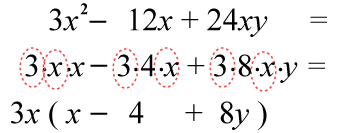
Kvar inne i parentesen blir det som ”är kvar” i varje term efter att du brutit ut gemensamma faktorer.
Viktigt att komma ihåg är att när du bryter ut är att när du bryter ut hela termens värde finns ändå en etta kvar i parentesen.
Till exempel om du ska bryta ur $4x$4x ur uttrycket $8x^2+4x$8x2+4x så får vi produkten $4x\left(2x+1\right)$4x(2x+1)som resultat och INTE $4x\left(2x\right)$4x(2x)!
I Matematik 2 ska du kunna faktorisera uttryck med hjälp av konjugat- och kvadreringsreglerna.
Tänk även på att du kan utnyttja möjlighet att bryta ut en minus etta för att få ombytta tecken på dina termer.
Exempelvis är $\left(a-b\right)=\left(-1\right)\left(-a-\left(-b\right)\right)=-\left(b-a\right)$(a−b)=(−1)(−a−(−b))=−(b−a) .
Det kan komma till användning när du ska förenkla uttryck med både täljare och nämnare.
Potensekvationer
När du löser potensekvationer underlättar det om du kan potenslagarna. Gärna utantill. I denna kurs använder vi oss framför allt av regeln att
$a^{\frac{1}{n}}=\sqrt[n]{a}$a1n =n√a
$\frac{1}{n}$1n kallas för exponentens inverterade värde eller exponentens invers.
I en potensekvation är alltid variabeln i basen.
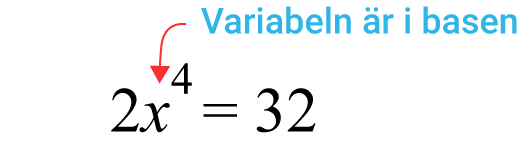
Om potensekvationen har en jämn exponent, finns det en negativ och en positiv lösning.
Om potensekvationen har en udda exponent, finns det endast en lösning.
Du löser ekvationen antingen med $n:$n:te roten ur båda leden eller upphöjer vänster och högerledet till $\frac{1}{n}$1n .
Vilket du vill använda väljer du själv, då dessa två är desamma enligt potenslagen. Det är oftast lättare att använda potensformen i stället för roten när du ska lösa ekvationen utan digitalt hjälpmedel. Detta beror på att du ofta kan förenkla uttrycket med potenslagarna, innan du genomför själva beräkning.
Fem sätt att lösa andragradsekvationer på
Tänk på att aldrig dividera bort en variabel när du löser ekvationer. Du riskerar att förlora lösningar!
En andragradsekvation kan ha noll, en eller två lösningar. Lösningarna kallas för rötter. I denna kurs har vi lärt oss fem metoder för att lösa andragradsekvationer.
Kvadratrotsmetoden
Andragradsekvationer som saknar en förstagradsterm kan lösas med kvadratrotsmetoden.
$ax^2+c=0$ där $a$ och $c$ är konstanter skilda från noll.
Exempelvis är ekvationen $2x^2-8=0$2x2−8=0 en mycket lämplig ekvation för att tillämpa kvadratrotsmetoden på.
Observera att $\sqrt{a}$√a endast har ett värde. Men vid ekvationslösning kan det däremot finnas två olika lösningar, nämligen även den negativa roten. Detta eftersom att ett negativt tal upphöjt i två blir ett positivt tal.
Nollproduktmetoden
Andragradsekvationer som saknar en konstatterm kan lösas med nollproduktmetoden.
$ax^2+bx=0$ där $a$ och $b$ är konstanter skilda från noll.
Exempelvis är ekvationen $2x^2-8x=0$2x2−8x=0 en mycket lämplig ekvation för att tillämpa nollproduktmetoden på.
PQ-formeln/Lösningsformeln
Andragradsekvationer som både har en andragradsterm, en förstagradsterm och en konstantterm kan lösas med lösningsformeln eller kvadratkompetering.
$ax^2+bx+c=0$ där $a,$ $b$ och $c$ är konstanter skilda från noll.
Exempelvis är ekvationen $x^2+4x-5=0$x2+4x−5=0 en mycket lämplig ekvation för att tillämpa pq-formeln på. Den säger att
$x^2+px+q=0$x2+px+q=0 har lösningarna $x_{1,2}=$x1,2= $-\frac{p}{2}\pm\sqrt{\left(\frac{p}{2}\right)^2-q}$−p2 ±√(p2 )2−q
Tänk på att alltid kontrollera att ena ledet är lika med noll och koefficienten framför andragradstermen lika med ett innan du sätter in dina värden i formeln!
Tips
För alla andragradsekvationer gäller att $p=-\left(x_1+x_2\right)$p=−(x1+x2) och $q=x_1\cdot x_2$q=x1·x2 där $x_1$x1 och $x_2$x2 motsvarar rötterna till andragradsekvationen och $p$p och $q$q syftar på ekvationen omskriven på formen $x^2+px+q=0$x2+px+q=0.
Andragradsekvationer på allmänform
När andragradsfunktioner är skriven på allmänform
$ax^2+bx+c=0$ax2+bx+c=0 kan du, i stället för att först skriva om formeln redo för PQ, direkt välja att använda formeln $x_{1,2}=$x1,2= $-\frac{b}{2a}$−b2a $\pm\frac{\sqrt{b^2-4ac}}{2a}$±√b2−4ac2a för att lösa ekvationen.
Grafisk lösning
Grafisk lösning går ut på att rita HL och VL som två olika funktioner och sedan läsa av skärningspunkternas $x$x-värden. De motsvarar nämligen ekvationens lösning. Finns inga skärningspunkter saknar ekvationen reella lösningar. I exemplet nedan söks lösningen till $f(x)=0$ƒ (x)=0, alltså parabelns nollställen.
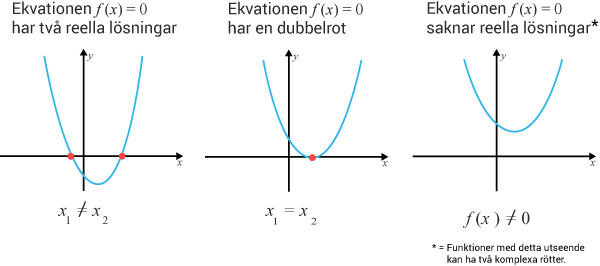
Rotekvationer och falska rötter (Ma2c)
När man löser en rotekvation med kvadrering kan även en så kallad falsk rot smyga sig med. Alltså en rot som inte ger en likhet i ursprungs ekvationen. Testa därför alltid dina rötter i den ursprungliga ekvationen när du behöver kvadrera för att lösa ekvationen.
Logaritmer
Logaritmer gör det möjligt att lösa exponentialekvationer algebraiskt. Med hjälp av logaritmlagar kan vi skriva om ekvationer så att variabler som funnits i exponenten hamnar i basen. Det innebär att logaritmen är den inversa funktionen till exponentiering.
För att hänga med i tanken vid ekvationslösningen kan en mening hjälpa. $\lg$lg kan utläsas som ”det tal tio ska upphöjas till för att bli…”
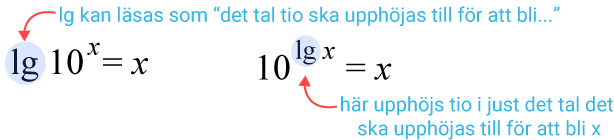
På så sätt kan vi lösa ekvationen med hjälp av logaritmer.

Men denna loop av omskrivningar kan vi nu lösa uppgifter med logaritmer på olika former.
$y=10^x$y=10x $\Leftrightarrow$ $\lg y=\lg10^x$lgy=lg10x $\Leftrightarrow$ $\lg y=x$lgy=x $\Leftrightarrow$ $10^{\lg y}=10^x$10lgy=10x $\Leftrightarrow$ $y=10^x$y=10x
Funktioner och samband
Räta linjens ekvation i k-form
En förstagradsfunktion kallas även för en linjär funktion och dess graf är en rak linje, en så kallad rät linje. Den kan beskrivas matematiskt med likheten y = kx + m där bokstäverna i formeln betyder följande.
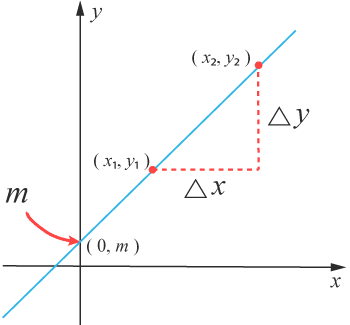
- k är en konstant som motsvarar linjens lutning. Konstanten kallas även riktningskoefficienten.
- m är en konstant som motsvarar -värdet där linjen skär -axeln.
- $x$x och $y$y variablerna i funktionen som ger alla punkter $\left(x,\text{ }y\right)$(x, y) på grafen.
Värdet på konstanten $k$k, som alltså motsvarar linjens lutning, kan bestämmas med hjälp av två valfria punkter på linjen. $\bigtriangleup y$△y motsvarar förändringen i $y$y -led och $\bigtriangleup x$△x förändringen i $x$x -led mellan de två punkterna.
$k=$k= $\frac{\bigtriangleup y}{\bigtriangleup x}=\frac{y_2-y_1}{x_2-x_1}$△y△x =y2−y1x2−x1
I denna kurs ska du kunna bestämma det räta linjens ekvation samt ange en mängd olika egenskaper linjen har.
Positiv lutning – $y$y-värdet ökar när $x$x-värde ökar. I räta linjens ekvation är $k>0$k>0.
Negativ lutning – $y$y-värdet minskar när $x$x-värde ökar. I räta linjens ekvation är $k<0$k<0.
Lutning lika med noll – $y$y-värdet blir oförändrat när $x$x-värde ökar. I räta linjens ekvation är $k=0$k=0 .
Saknar lutning – grafen motsvarar en lodrät linje och ingen funktion. En sådan linjens ekvation är $x=a$x=a där $a$a motsvarar värdet där grafen skär $x$x -axeln.
Alla punkter $\left(x,\text{ }y\right)$(x, y) som ger att likheten $y=kx+m$y=kx+m stämmer ligger på linjen.
Parallella linjer
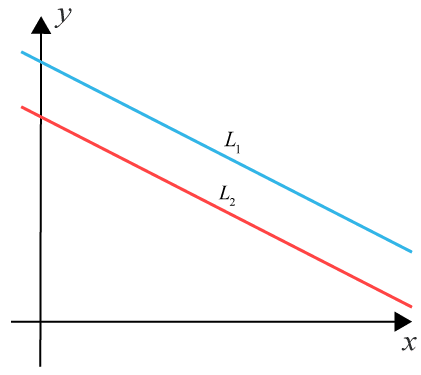
Två linjer $L_1=k_1x+m_1$L1=k1x+m1 och $L_2=k_2x+m_2$L2=k2x+m2 är parallella då de har samma lutning.
Alltså då $k_1=k_2$k1=k2
Vinkelräta linjer
Två linjer $L_1=k_1x+m_1$L1=k1x+m1 och $L_2=k_2x+m_2$L2=k2x+m2 är vinkelräta då de har en vinkel mellan dem som är $90^{\circ}$90∘.
Detta gäller då $k_1\cdot k_2=-1$k1·k2=−1
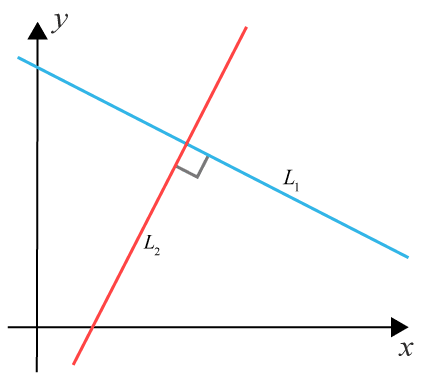
Som följa av detta kan du därmed undersöka om linjer är parallella eller vinkelräta genom att jämföra linjernas $k$k -värden.
Räta linjens ekvation i allmänform
$ax+by+c=0$ax+by+c=0 , där inte både $a$a och $b$b är noll
Linjära ekvationssystem
När du löser ekvationssystem söker du finna koordinaterna för punkter där linjerna skär, eller korsar, varandra.
Lösningen till ett linjära ekvationssystem är därmed koordinaterna för linjernas skärningspunkter. Du anger både $x$x -värdet och $y$y -värdet i din lösning.
Ett linjärt ekvationssystem har inga, exakt en eller oändligt antal lösningar. Det är linjernas $k$k– och $m$m-värde som avgör vilket sm gäller.
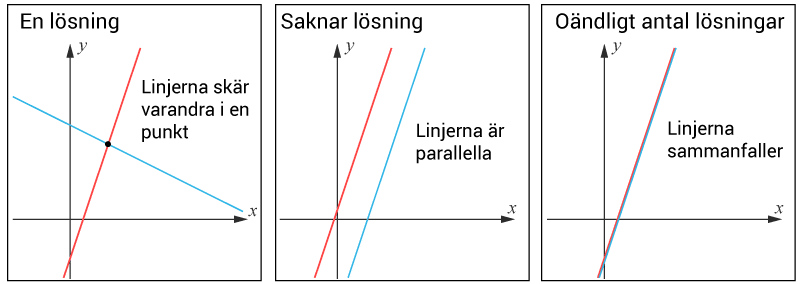
Ekvationssystemet har exakt en lösning då linjerna har olika lutning. Alltså då $k_1\ne k_2$k1≠k2. Linjerna kan har både samma eller olika $m$m-värde utan att det påverkar resultatet, så länge lutningen är olika.
Då linjerna är parallella, men inte sammanfallande, har ekvationssystemet inga lösningar. Man säker att det saknar lösningar. Detta inträffar då linjerna har samma lutning, men olika $m$m -värden. Alltså då $k_1=k_2$k1=k2 och $m_1\ne m_2$m1≠m2.
Ett linjärt ekvationssystem har oändligt antal lösningar då de bägge ekvationerna representerar samma linje. Alltså då $k_1=k_2$k1=k2 och $m_1=m_2$m1=m2.
Vi har i denna kurs introducerats för grafiska lösningsmetoder och två algebraiska, substitutionsmetoden och additionsmetoden. Återvänd till lektionerna för att repetera hur du löser ekvationssystem med hjälp av dess metoder.
Polynom
Polynom är en summa av termer där variabeln är i basen och alla exponenter tillhör de naturliga talen. Alla polynom kan skrivas i faktorform.
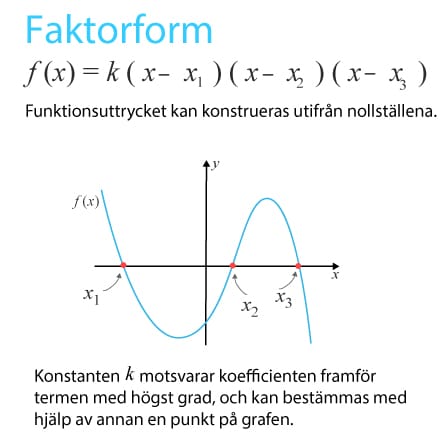
Andragradsfunktioner
Andragradsfunktion är en funktionens funktionsuttryck är ett andragradspolynom. Det innebär att alla andragradsfunktioner kan skrivas på formen
$y=ax^2+bx+c=0$y=ax2+bx+c=0 där $a\ne0$a≠0. Andragradsfunktionen graf kallas för en parabel.

Koefficienten $a$a avgör om funktionen är positiv eller negativ. Just större värde på $a$a, ju smalare blir parabeln. Parabeln förflyttas i sid och höjdled då värdet på $b$b förändras. Medan konstanten $c$c endast förskjuter parabeln i höjdled. Värdet på $c$c är alltid detsamma som $y$y -värdet för parabelns skärningspunkt med $y$y-axeln.
Vertex
Då $a>0$a>0 är andragradsfunktionen positiv. Grafen är öppen uppåt, en glad mun. Parabeln har en minimipunkt.
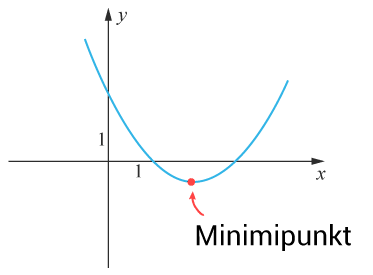
Då $a<0$a<0 är andragradsfunktionen negativ. Grafen är öppen nedåt, en sur mun. Parabeln har en maximipunkt.
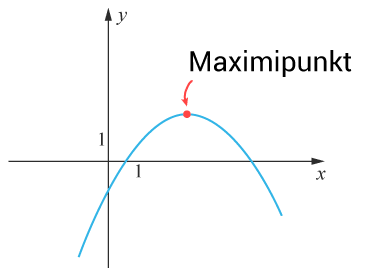
Maximipunkten och minimipunkten har samlingsnamnet vertex.
Parabelns största och minsta värde
Vertex har alltid koordinaten $\left(x_s,\text{ }f\left(x_s\right)\right)$(xs, ƒ (xs))där $x_s$xs motsvarar $x$x -värdet där symmetrilinjen skär $x$x-axeln, eller med andra ord symmetrilinjens ekvation, och $f\left(x_s\right)$ƒ (xs) är största eller minsta funktionsvärdet.
Parabeln största eller minsta värde återfinns alltid i vertex. Du kan beräkna värdet $f\left(x_s\right)$ƒ (xs) genom att sätta in symmetrilinjens ekvation i funktionsuttrycket.
Nollställen
De $x$-värden där parabeln skär $x$-axeln kallas för nollställen.
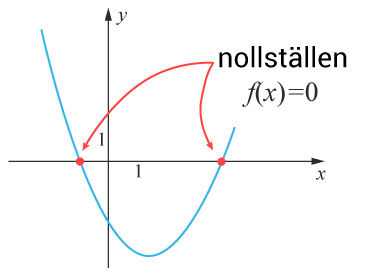
Parabeln kan ha noll, en eller två nollställen.
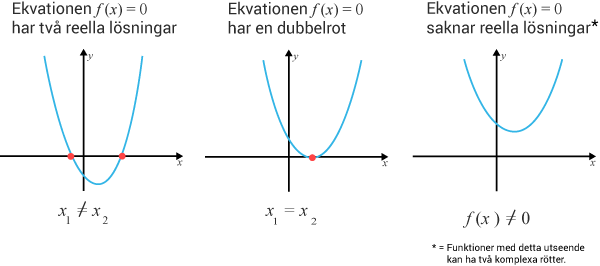
Parabeln har två nollställen då $\left(\frac{p}{2}\right)^2>q$(p2 )2>q
ett nollställe då $\left(\frac{p}{2}\right)^2=q$(p2 )2=q $$
och saknar nollställen då $\left(\frac{p}{2}\right)^2<$(p2 )2< $q$q.
Symmetrilinjens ekvation
En parabel är alltid symmetrisk och genom vertex går parabelns symmetrilinje.
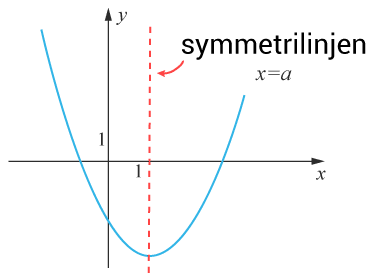
Symmetrilinjens ekvation är $x=a$x=a , där $a$a motsvarar $x$x -värdet där symmetrilinjen skär $x$x-axeln. Vi har lärt oss att följande två kvoter ger oss ekvationen.
$x_s=$xs= $-\frac{p}{2}$−p2 och $x_s=$xs= $\frac{x_1+x_2}{2}$x1+x22
där $p$p syftar på lösningsformeln och $x_1$x1 och $x_2$x2 är två punkter på parabeln med samma $y$y-värde. Exempelvis nollställena.
Potensfunktioner
Alla funktioner där variabeln återfinns i basen är potensfunktioner. De kan alla skrivas som en summa av termer på formen
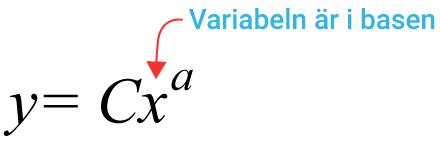
De vi jobbat extra mycket med i denna kurs är de linjära funktionerna $y=kx+m$y=kx+m och andragradsfunktionerna $y=ax^2+bx+c$y=ax2+bx+c som båda är exempel på potens funktioner. I Ma2c har vi även lärt oss lösa rotekvationer $y=C\cdot\sqrt[n]{a}$y=C·n√a som är ännu ett exempel på en potensfunktion.
Exponentialfunktioner
De funktioner där variabeln återfinns i exponenten är exponentialfunktioner. De kan alla skrivas som en summa av termer på formen
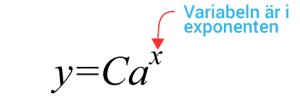
där $a>0$a>0 och $a\ne1$a≠1
$y$y motsvarar funktionsvärdet
$C$C motsvarar startvärdet, funktionens värde när $x=0$x=0
$a$a motsvarar förändringsfaktorn
$x$x motsvarar ofta antalet förändringar
Exponentialfunktioner är effektiva att använda då man har procentuella förändringar som upprepas sig.
Växande då $C$C och $a>1$a>1. Förändringsfaktorn motsvarar en procentuell ökning.
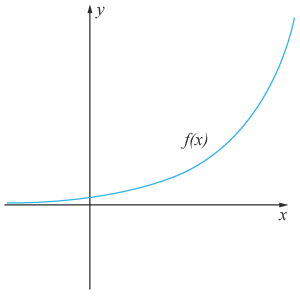
Avtagande då $C$C är positivt och $0<$0< $a<1$a<1. Förändringsfaktorn motsvarar en procentuell minskning.
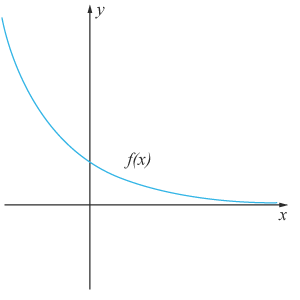
Om $C$C är ett negativa tal kommer grafen speglas i $x$x -axeln. Du kan med fördel undersöka exponentialfunktionens utseende genom att skriva in olika värden på $C$C och $a$a i ett digitalt hjälpmedel. Exempelvis grafritaren här till höger på sidan.
Geometri
I Matematik 2a, 2b och 2c lära du dig några nya geometriska satser samt att genomföra bevis. Här kommer några av dem.
Skala (Ma2c)
Med hjälp av en skalfaktor kan vi bestämma hur areor och volymer förändras vid förstoringar och förminskningar.
$\text{Skalfaktor}=$Skalfaktor= $\frac{\text{Bild}}{\text{Verklighet}}$BildVerklighet
Kvoten kan även skrivas som $\text{Bild : Verklighet}$Bild : Verklighet. Om talet till vänster om kolonet är störst motsvarar det en förstoring och tvärt om, om talet till vänster om kolonet är mindre motsvarar det en förminskning.
Vi får area- och volymskalan med följande likheter.
$\text{Areaskala =(Längdskala)}^2$Areaskala =(Längdskala)2
$\text{Volymskala =(Längdskala)}^3$Volymskala =(Längdskala)3
Vet du exempelvis att längdskalan är $1:4$1:4 kommer areaskalan vara $\left(1:4\right)^{^2}=1:16$(1:4)2=1:16 och volymskalan $\left(1:4\right)^3=1:64$(1:4)3=1:64.
Likformighet
Trianglarna $\bigtriangleup ABC$△ABC och $\bigtriangleup DEF$△DEF är likformiga om de har samma form. Det har de då två av trianglarnas vinklar är lika stora. För likformiga trianglar gäller att likbelägna sidorna, alltså sidor mellan de vinklar som är lika stora, förhåller sig mot varandra enligt nedan.
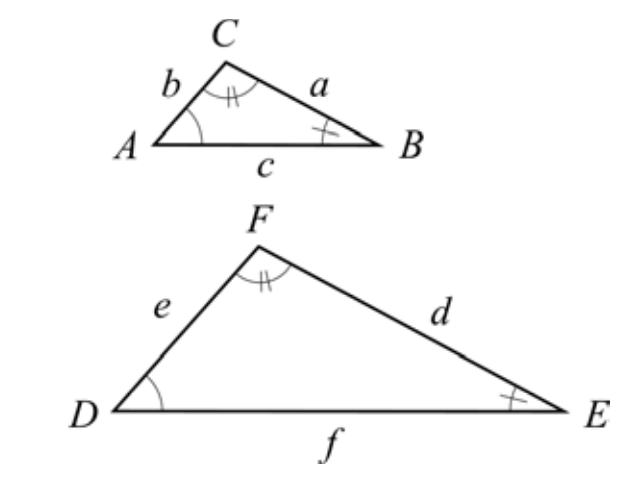
$\frac{a}{d}=\frac{b}{e}=\frac{c}{f}$ad =be =cƒ
Man använder skrivsättet $\bigtriangleup ABC\text{ }\simeq\text{ }\bigtriangleup DEF$△ABC ≃ △DEF för att ange att de två trianglarna är kongruenta.
Kongruens (Ma2b,c)
Två trianglar är kongruenta om de har samma form OCH storlek. Med hjälp av att kolla att något av följande tre gäller för trianglarna $\bigtriangleup ABC$△ABC och $\bigtriangleup DEF$△DEF kan vi bestämma kongruens mellan dem.
1. Alla sidor överensstämmer
2. Två sidor och den mellanliggande vinkeln överensstämmer
3. Två vinklar och den mellanliggande sidan överensstämmer
Man använder skrivsättet △ABC ≅ △DEF för att ange att de två trianglarna är kongruenta.
Topptriangel- och transversalsatsen
Som följd av likformighet får vi topptriangelsatsen och transversalsatsen.
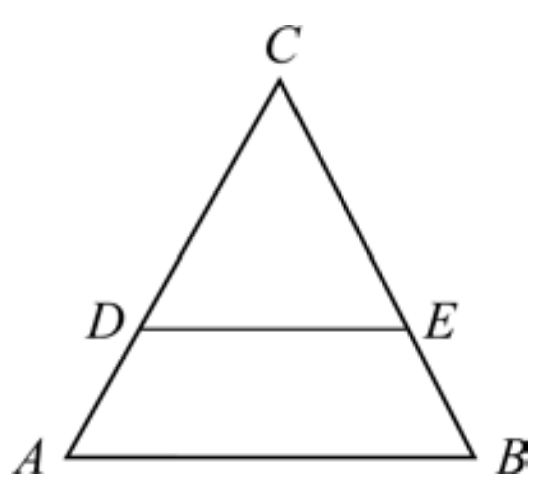
Om $DE$DE är parallell med $AB$AB är $DE$DE en parallelltransversal och delar triangeln i en topptriangel $\bigtriangleup ADE$△ADE och en parallelltrampets. Topptriangelsatsen säger då att likbelägna sidor i triangeln $\bigtriangleup ABC$△ABC och sidor i topptriangeln $\bigtriangleup ADE$△ADE förhåller sig till varandra enligt
$\frac{DE}{AB}=\frac{CD}{AC}=\frac{CE}{BC}$DEAB =CDAC =CEBC
Som följd av likformighet får vi även att de sidor i triangeln $\bigtriangleup ABC$△ABC som delas av parallelltransversalen förhåller sig mot varandra som följer
$\frac{CD}{AD}=\frac{CE}{BE}$CDAD =CEBE
Observera att detta förhållande endast gäller de ”delade” sidorna och inte den sida om inte delats av parallelltransversalen.
Bisektrissatsen
En rät linjen genom en en vinkelspets som dela vinkeln i två lika stora delar är en bisektris.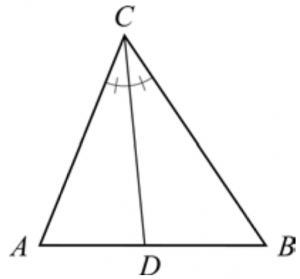
Bisektrisen delar den motstående sidan i två delar som förhåller sig mot vinkelbenen som följer.
$\frac{AD}{BD}=\frac{AC}{BC}$ADBD =ACBC
Vinklar
Då $L_1$L1 skär de två parallella linjerna $L_2$L2 och $L_3$L3 uppstår olika några vinklar. Nedan ser du vad de kallas och hur de förhåller sig till varandra.
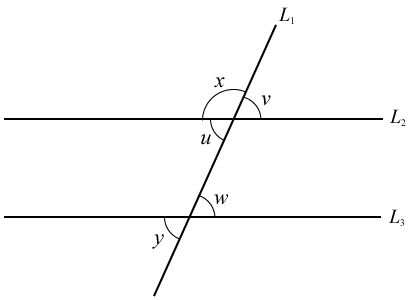
Vinklar som tillsamman bildar en rak vinkel kallas sidovinklar. I figuren $u$u och $v$v är sidovinkar vilket ger att $u+v=180^{\circ}$u+v=180∘
Vinklar som uppstår mitt emot varandra vid två linjer skärningspunkt kallas vertikalvinklar. De är lika stora. Alltså är $w=v$w=v och även $y=w$y=w.
Vinklar som ligger ”på samma ställe” vid de två olika skärningspunkterna kallas likbelägna. Även de är lika stora. Så $v=w$v=w och $y=u$y=u
Vinklar som är som ”förskjuta” vertikalvinklar kallas alternatvinklar. Även de är lika stora. Alltså gäller att $u=w$u=w.
Observera att detta endast gäller då $L_2$L2 och $L_3$L3 är parallella.
Kordastasten
En korda är en rät linje mellan två punkter på cirkelbågen. Diametern är en korda som går genom cirkelns mittpunkt. När två kordor skär varandra förhåller sig delarna som uppstår på följande vis.

$ad=cd$ad=cd
Randvinkelsatsen
Randvinkeln i en cirkel är en vinkeln mellan två kordor som träffar varandra i en punkt som ligger på cirkeln. Medelpunktsvinkeln är vinkeln i cirkelns medelpunkt mellan radierna till två punkter på cirkelbågen.

Då en medelpunktsvinkel och randvinkel utgår från samma cirkelbåge är alltid medelpunktsvinkeln dubbels så stor som randvinkeln. Sambandet kallas för randvinkelsatsen och säger att $y=2x$y=2x
Pythagoras sats
I en rätvinklig triangel gäller Pythagoras sats som säger att $a^2+b^2=c^2$a2+b2=c2
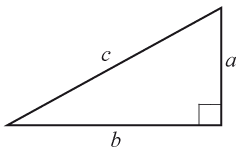
där $a$a och $b$b kallas katetrar och $c$c hypotenusan. Hypotenusan är alltid triangelns längsta sida.
Trigonometri (Ma2a)
Med hjälp av trigonometri kan vi beräkna triangelns okända vinklar och längder. Sambanden mellan vinklar och sidor kan sammanfattas så här.
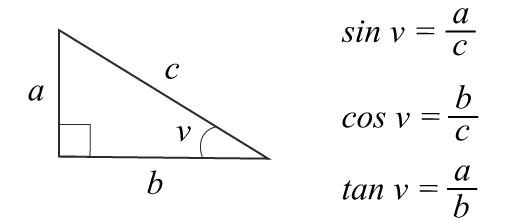
Den vinkel som utgör ett vinkelben till vinkeln $v$v kallas närliggande. Den sida som inte utgår från vinlek kallas motstående.
Avståndsformeln
Med hjälp av avståndsformeln kan vi bestämma avståndet $d$d mellan två punkter $\left(x_1,\text{ }y_1\right)$(x1, y1) och $\left(x_2,\text{ }y_2\right)$(x2, y2) i planet.
$d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}$d=√(x2−x1)2+(y2−y1)2
Egentligen är det bara en omskrivning av Pythagoras sats.
Mittpunktsformeln
Med hjälp av mittpunktsformeln kan vi bestämma den punkt $\left(x_m,\text{ }y_m\right)$(xm, ym) som ligger mitt emellan de två punkterna $\left(x_1,\text{ }y_1\right)$(x1, y1) och $\left(x_2,\text{ }y_2\right)$(x2, y2) i planet.
$x_m=$xm= $\frac{x_1+x_2}{2}$x1+x22 och $y_m=$ym= $\frac{y_1+y_2}{2}$y1+y22
Statistik (Ma2b,c)
I matematik 2 introducerar vi ett antal nya begrepp i statistiken och lär oss granska och värdera statistik material med hjälp av dessa.
Population
Hela mängden individer, objekt eller element som ingår i undersökningen.
Urval
Den metod man använder för att plocka ut stickprovet. Det finns flera olika sätt att göra urval på. Bland annat slumpmässiga urval. Du kan då välja på att antingen göra obundet slumpmässigt urval eller stratifierat urval.
Obundet slumpmässigt urval
Alla individer, enheter eller element i populationen har samma sannolikhet att hamna i stickprovsundersökningen.
Stratifierat urval
Urvalet görs så att alla delgrupper finns representerade i samma proportioner som i den hela populationen.
Stickprovsundersökning
Undersökning på en del av populationen.
Totalundersökning
Undersökning på en hel population.
Frekvens
Antal observationer för ett visst observationsvärde.
Relativ frekvens
Frekvens angiven som andel. Ofta i procent.
Felkällor
Olika saker som kan påverka så att resultatet blir missvisande (fel) vid en statistisk undersökning. Exempelvis bortfall och mätfel.
Bortfall
Den del av urvalet eller populationen som inte ger något resultat. Till exempel inte svarar på en undersökning.
Felmarginal
Med hjälp av följande formel försöker man säkerställa att en undersökning är tillförlitlig.
$f=1,96\cdot$ƒ =1,96· $\sqrt{\frac{p\left(100-p\right)}{n}}$√p(100−p)n
där $n$n är stickprovets storlek och $p$p den procentuella andelen av populationen.
Om ett resultat av en undersökning landar i intervallet för felmarginalen anses undersökningen vara statistiskt säkerställd.
Lägesmått
Lägesmått är värden som sammanfattar alla mätvärden i en datamängd med ett enda representativt värde. I matematik 2 behöver du kunna beräkna och bestämma lägesmåtten medelvärde, median och typvärde både utifrån tabeller och datamängder.
Medelvärde
$\text{Medelvärdet}=$Medelvärdet= $\frac{\text{Summan av alla observationsvärden}}{\text{Antal observationer}}$Summan av alla observationsvärdenAntal observationer
Median
Mittenvärdet i datamängden när den står i storleksordning. Vid jämnt antal värden blir medianvärdet medelvärdet av de två mittersta värdena.
Typvärde
Typvärdet är det vanligast förekommande observationsvärdet i en datamängd.
Spridningsmått
Spridningsmått anger hur observationerna i datamängden varierar kring lägesmåttens värden. I matematik 2b och 2c ska du kunna beräkna och bestämma spridningsmåtten variationsbredd, kvartilavstånd och percentiler samt känna till hur man kan beräkna standardavvikelser och jobba med normalfördelat material.
Standardavvikelse för stickprov
Standardavvikelsen kan ses som ett mått på en genomsnittlig avvikelse från medelvärdet.
Den beräknas med följande formel
$s=$s= $\sqrt{\frac{\left(x_1-\overline{x}\right)^2+\left(x_2-\overline{x}\right)^2+…+\left(x_n-\overline{x}\right)^2}{n-1}}$√(x1−x)2+(x2−x)2+…+(xn−x)2n−1
där
$s$s är standardavvikelse
$x_n$xn är observationsvärdena
$\overline{x}$x är medelvärdet
$n$n är antal observationer
Ju större värde på standardavvikelsen, ju större spridning på mätvärdena.
Normalfördelning
Normalfördelningskurvan visar hur en normalfördelad datamängd fördelar sig kring medelvärdet.
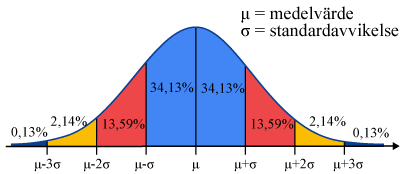
I ett normalfördelat material är medelvärdet och medianen samma värde. I matematik 2 ska du kunna beräkna och bestämma förväntade mängder och sannolikheter på normalfördelat material med hjälp av klockkurvan.
Lådagram
Ett lådagram är ett sätt att visa en datamängds spridning. Lådagrammet delar upp datamängden i fyra lika stora delar som kallas för kvartiler. Det leder till att varje kvartil motsvarar $25\%$25% av datamängden. Kvartilen $Q_2$Q2 motsvarar datamängdens median.
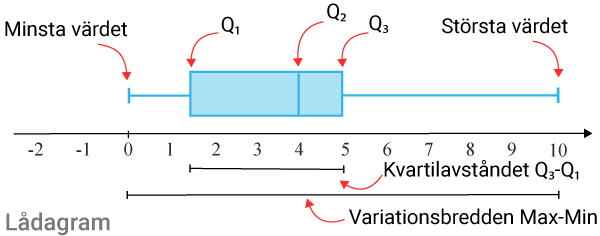
Repetitionsmaterial
Tyvärr kommer du inte att få tillgång till all information som delas här, i sammanfattning Matematik 2, vid Nationella provet. Följ länken för att se den Formelsamling du får använda vid Nationella provet Matematik 2.
Använd gärna några av våra kapiteltest för att repetera och fördjupa dina kunskaper. Samtliga uppgifter har fullständiga förklaringar.
Kapiteltest – Algebra Ma2a
Kapiteltest – Algebra Ma2b
Kapiteltest – Algebra Ma2c
Kapiteltest – Linjära funktioner och ekvationssystem Ma2a
Kapiteltest – Linjära funktioner och ekvationssystem Ma2b
Kapiteltest – Linjära funktioner och ekvationssystem Ma2c
Kapiteltest – Andragradsekvationer Ma2a
Kapiteltest – Andragradsekvationer Ma2b
Kapiteltest – Andragradsekvationer Ma2c
Kapiteltest – Exponential- och Potensfunktioner Ma2a
Kapiteltest – Exponential- och Potensfunktioner Ma2b
Kapiteltest – Exponential- och Potensfunktioner Ma2c
Kapiteltest – Statistik Ma2a
Kapiteltest – Statistik Ma2b
Kapiteltest – Statistik Ma2c
Kapiteltest – Geometri Ma2a
Kapiteltest – Geometri Ma2b
Kapiteltest – Geometri Ma2c
Prov Centrala begrepp Ma2 Del 1
Prov Centrala begrepp Ma2 Del 2
Prov Centrala begrepp Ma2 Del 3
Vill du träna fler uppgifter på en särskild betygsnivå eller ett centralt innehållsområde så använd vår uppgiftsgenerator.
Här kan du hitta alla gamla nationella prov att öva på.

Endast Premium-användare kan kommentera.