Kirchhoffs Strömlag

Exempel 1

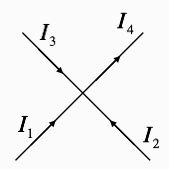
Beräkna den utgående strömmen från noden i bilden nedan givet att $I_1 = 0,35$ A, $I_2 = 0,60$ A samt $I_3=1,20$ A.

Lösning

Strömmen in ska vara lika stor som strömmen ut.

Strömmen in är: $I_1 + I_2 + I_3$.

Strömmen ut är: $I_4$.

Detta ger oss att: $I_4 =I_1 + I_2 + I_3 = 0,35 + 0,60 + 1,20 = 2,15$ A.

Den utgående strömmen är på $2,15$ A.

Exempel 2

Beräkna strömmen $I_5$ i bilden givet att: $I_1 = 2,5$ A, $I_2=1,8$ A samt $I_4=1,5$ A.

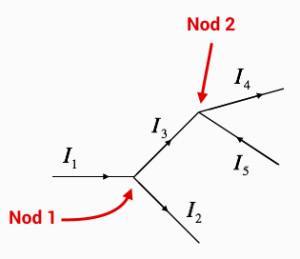
Lösning

I denna uppgift får vi använda Kirchhoffs strömlag två gånger.

Nod 1:

$I_1 = I_2 + I_3$

$2,5 = 1,8 + I_3$

$I_3 = 0,70$.

Nod 2:

$I_3 + I_5 = I_4$

$0,70 + I_5 = 1,5$

$I_5 = 0,80$ A.

Vilket alltså är svaret.

(Observera att vi i videon borde använt två värdesiffror i svaret och inte en.)