Författare: Simon Rybrand
Simon Rybrand
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Uppgifter i videon
- I figuren nedan (se bild i video) visas det område som begränsas av kurvan y=4−ex och koordinataxlarna.
När området roteras runt x-axeln bildas en rotationskropp.
Teckna ett uttryck för rotationskroppens volym och bestäm dess värde med minst tre värdesiffror.
(Uppgift 20 har utgått från Ma4)
20. En fågelunge faller från en 8,0m hög klippa. För att förenklat beskriva fallrörelsen kan följande differentialekvation
ställas upp:dtdv+5v=10där v är fallhastigheten i m/s efter tiden t sekunder.
a) Visa att v(t)=2−2e−5t är en lösning till differentialekvationen.
b) Bestäm tiden det tar för fågelungen att falla 8,0m
Formler och begrepp som används i video och övningar
Volymintegraler metod
Det finns ett sätt att tänka strukturerat kring beräkning av volymintegraler. Det handlar övergripande om att:
- Börja med att först ta fram en formel för att beräkna volymen för en skiva.
- Detta gör du genom att först välja om du skall beräkna den i x–led eller i y–led. Om du beräknar den i x–led får du bredden Δx och i y – led bredden Δy på skivan. Ställ sedan upp en formel för att beräkna volymen för en skiva.
- Använd en integral för att beräkna volymen (summera alla skivors volym) för hela kroppen.
Integralkalkylens fundamentalsats
a∫bf(x)dx=[F(x)]ab=F(b)–F(a) där
- a är den undre gränsen och b den övre.
- f(x) är integranden, dvs den funktion vi tar fram primitiv funktion F(x) på.
- För att få fram värdet på integralen beräknas sedan F(b) – F(a)
Kommentarer
e-uppgifter (1)
1.
(2/0/0)INGÅR EJE C A B 1 P 1 PL M R K Är y=e−3x en lösning till differentialekvationen y′′+3y′=0?
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
c-uppgifter (1)
2.
(0/1/0)E C A B P 1 PL M R K 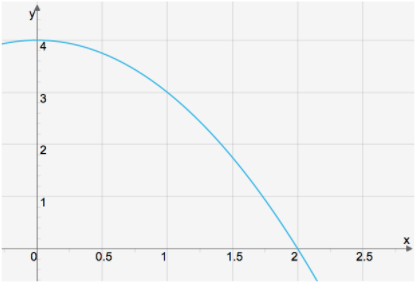
Området i figuren begränsas av y=−x2+4y=−x2+4 och koordinataxlarna. När området roteras runt xx -axeln bildas en rotationskropp.
Bestäm dess volym.
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Eddler
POPULÄRA KURSER
FÖRETAGSINFO
Eddler AB
info@eddler.se
Org.nr: 559029-8195
Kungsladugårdsgatan 86
414 76 Göteborg

Magnus Adler
I uppgift 2 står det π((32/5 − 64/3 +32)−0) ≈17 v.e
Jag får detta till π(17,06666667).
Har jag missat något, eller har ert svar blivit fel?
Mvh
Magnus
Simon Rybrand (Moderator)
Jepp, det fattas π där.
Det är nu korrigerat
Amanda Jansson
Hej. Övning 1 till den här videon verkar fel. Uträckningen säger att det ska vara y^2 men den räknar bara med y i integralen.
Om man kunde få rätt lösning (om det nu är fel som står) så skulle det uppskattas. Vill se om jag har rätt när uppgiften görs på rätt sätt.
Simon Rybrand (Moderator)
Hej
Den var felaktig och jag har nu korrigerat denna, tack för att du sade till!
Endast Premium-användare kan kommentera.