Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Matematik 4
/ Komplexa tal och Polynom
Komplexa tal på Polär form
I den här lektionen lär vi oss hur vi skriver ett komplext tal $z=a+bi$z=a+bi på polär form.
Polär form
Ett komplext tal $z=a+bi$z=a+bi kan representeras av en vektor, som ritas i det komplexa talplanet. Ett annat sätt att definiera vektorn är att ange dess längd och dess vinkel i förhållande till den positiva reella axeln. Detta kallas polär form. En av fördelarna med denna form är att det blir enklare att dividera, multiplicera och framförallt beräkna potenser med komplexa tal. Ett annat användningsområde är att vi kan använda polär form för att lösa ekvationer av typen $z^n=w$zn=w.
Omskrivning till polär form
För att skriva ett komplext tal på polär form behövs alltså vektorns längd, det vill säga absolutbeloppet, samt vinkeln mellan den positiva reella talaxeln och det komplexa talets vektor. Denna vinkel kallas för argumentet.
Komplext tal på polär form
För ett komplext tal $z=a+bi$z=a+bi i första kvadranten gäller:
Absolutbeloppet ges av $|z|=|a+bi|=$|z|=|a+bi|= $\sqrt{a^2+b^2}$√a2+b2 och betecknas $r$r.
Argumentet (vinkeln) beräknas genom $v=\tan^{-1}(\frac{b}{a})$v=tan−1(ba ).
Det komplexa talet $z$z skrivs på polär form som
$z=r(\cos v+i\sin v)$z=r(cosv+isinv)
Exempel 1
Skriv det komplexa talet $q=2+4i$q=2+4i på polär form.
Lösning
Vi börjar med att åskådliggöra talet i det komplexa talplanet.
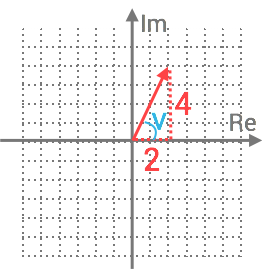
Absolutbeloppet: $|q|=\sqrt{2^2+4^2}=$|q|=√22+42= $\sqrt{4+16}=$√4+16= $\sqrt{20}$√20
Argumentet: $v=\tan^{-1}(\frac{4}{2})=1,10...\approx1,1$v=tan−1(42 )=1,10...≈1,1 rad
Alltså är $q$q på polär form: $q=\sqrt{20}(\cos1,1+i\sin1,1)$q=√20(cos1,1+isin1,1)
Om vi använder grader är argumentet $v\approx63^{\circ}$v≈63∘.
Argumentet beräknas på lite olika sätt, beroende på vilken kvadrant som det komplexa talet befinner sig i. När det gäller den första kvadranten kan argumentet bestämmas som i exemplet ovan. Men i de övriga tre kvadranterna behöver vi lägga till ytterligare ett steg. Först markeras vinkeln mellan vektorn och den reella axeln i den aktuella kvadranten. Denna vinkel kan bestämmas med hjälp av tangens. Därefter kan argumentet, som alltid utgår från den positiva reella axeln, beräknas. Nedan hittar du exempel kring detta för kvadranterna 2-4.
Exempel 2
Skriv det komplexa talet $ q = -3+4i $ på polär form.
Lösning
Vi börjar med att åskådliggöra talet i det komplexa talplanet.
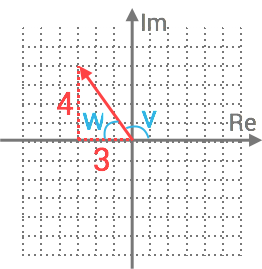
Absolutbeloppet: $|q|=\sqrt{3^2+4^2}=$|q|=√32+42= $\sqrt{9+16}=$√9+16= $\sqrt{25}=$√25= $5$5
Vektorn finns i den andra kvadranten, och argumentet beräknas då:
$v=\pi-w=$v=π−w= $\pi-\tan^{-1}(\frac{4}{3})=$π−tan−1(43 )= $2,21...\approx$2,21...≈ $2,2$2,2 rad
Alltså är $q$q på polär form: $q=5(\cos2,2+i\sin2,2)$q=5(cos2,2+isin2,2)
Om vi använder grader är argumentet $v\approx127^{\circ}$v≈127∘
Exempel 3
Skriv det komplexa talet $q=-4-5i$q=−4−5i på polär form.
Lösning
Vi börjar med att åskådliggöra talet i det komplexa talplanet.
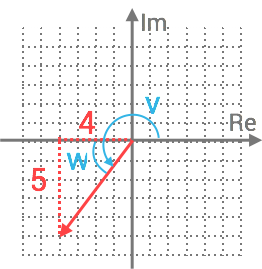
Absolutbeloppet: $|q|=\sqrt{4^2+5^2}=$|q|=√42+52= $\sqrt{16+25}=$√16+25= $\sqrt{41}$√41
Vektorn finns i den tredje kvadranten, och argumentet beräknas då:
$v=\pi+w=$v=π+w= $\pi+\tan^{-1}(\frac{5}{4})=$π+tan−1(54 )= $4,03...\approx$4,03...≈ $4,0$4,0 rad
Alltså är $q$q på polär form: $q=\sqrt{41}(\cos4,0+i\sin4,0)$q=√41(cos4,0+isin4,0)
Om vi använder grader är argumentet $v\approx231^{\circ}$v≈231∘.
Exempel 4
Skriv det komplexa talet $q=3-5i$q=3−5i på polär form.
Lösning
Vi börjar med att åskådliggöra talet i det komplexa talplanet.
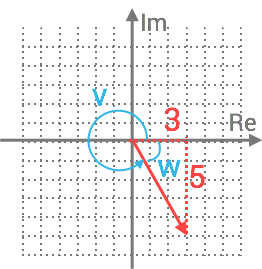
Absolutbeloppet: $|q|=\sqrt{3^2+5^2}=$|q|=√32+52= $\sqrt{9+25}=$√9+25= $\sqrt{34}$√34
Vektorn finns i den fjärde kvadranten, och argumentet beräknas då:
$v=2\pi-w=$v=2π−w= $2\pi-\tan^{-1}(\frac{5}{3})=$2π−tan−1(53 )= $5,25...°\approx$5,25...°≈ $5,3$5,3 rad
Alltså är $q$q på polär form: $q=\sqrt{34}(\cos5,3+i\sin5,3)$q=√34(cos5,3+isin5,3)
Om vi använder grader är argumentet $v\approx301^{\circ}$v≈301∘.
Exempel i videon
- Talet $ z=a+bi $ på polär form.
- Skriv om talet $ z=3+4i $ på polär form.
- Skriv $z = -4 + 5i$ på polär form.
- Skriv $z = -3 - 3i$ på polär form.
- Skriv $z = 4 - 4i$ på polär form.
Kommentarer
██████████████████████████
████████████████████████████████████████████████████
e-uppgifter (8)
-
1. Premium
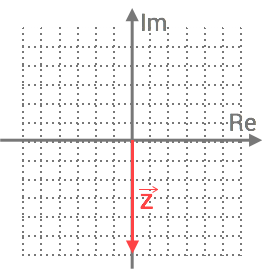
Vilket är argumentet för det markerade komplexa talet $z$z i figuren?
Svara i radianer.
Rättas inte automatiskt. Du bedömer själv mot facit.Svar:π²Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedöm ditt svarBedömningsanvisningar/Manuell rättningJämför med rätt svar ovan och kryssa i det du har fått med.Rätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...2. Premium
Vilket är absolutbeloppet för det komplexa talet $z$z som åskådliggörs som en vektor i det komplexa talplanet?
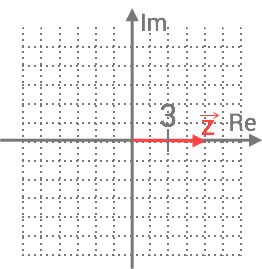Rättas inte automatiskt. Du bedömer själv mot facit.Svar:π²Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedöm ditt svarBedömningsanvisningar/Manuell rättningJämför med rätt svar ovan och kryssa i det du har fått med.Rätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...3. Premium
Låt $z=3-i$z=3−i, beräkna $r$r .
Bedöm ditt svarBedömningsanvisningar/Manuell rättningJämför med rätt svar ovan och kryssa i det du har fått med.Rätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...Din skolas prenumeration har gått ut!Din skolas prenumeration har gått ut!4. Premium
Skriv $z=1+2i$z=1+2i på polär form.
Bedöm ditt svarBedömningsanvisningar/Manuell rättningJämför med rätt svar ovan och kryssa i det du har fått med.Rätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...5. Premium
Hur kan vi beräkna realdelen på polär form?
Bedöm ditt svarBedömningsanvisningar/Manuell rättningJämför med rätt svar ovan och kryssa i det du har fått med.Rätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...6. Premium
Skriv $z=5-12i$z=5−12i på polär form
Bedöm ditt svarBedömningsanvisningar/Manuell rättningJämför med rätt svar ovan och kryssa i det du har fått med.Rätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...7. Premium
Skriv $z=-8+15i$z=−8+15i på polär form
Bedöm ditt svarBedömningsanvisningar/Manuell rättningJämför med rätt svar ovan och kryssa i det du har fått med.Rätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...8. Premium
Låt $z=4\left(\text{ }\cos\frac{\pi}{2}+i\text{ }\sin\frac{\pi}{2}\right)$z=4( cosπ2 +i sinπ2 ) .
Skriv $z$z på formen $z=a+bi$z=a+bi .
Bedöm ditt svarBedömningsanvisningar/Manuell rättningJämför med rätt svar ovan och kryssa i det du har fått med.Rätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...c-uppgifter (3)
-
9. Premium
Skriv talet $z=8-6i$z=8−6i på polär form.
Rättas inte automatiskt. Du bedömer själv mot facit.Svar:π²Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedöm ditt svarBedömningsanvisningar/Manuell rättningJämför med rätt svar ovan och kryssa i det du har fått med.Rätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Se mer:Videolektion: Komplexa tal på Polär formRättar...10. Premium
Bestäm $\text{arg }z$argz om $z=\frac{\sqrt{3}}{2}-\frac{i}{2}$z=√32 −i2 .
Rättas inte automatiskt. Du bedömer själv mot facit.Svar:π²Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedöm ditt svarBedömningsanvisningar/Manuell rättningJämför med rätt svar ovan och kryssa i det du har fått med.Rätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Se mer:Videolektion: Komplexa tal på Polär formRättar...11. Premium
Skriv talet $z=-\sqrt{5}+\sqrt{15}i$z=−√5+√15i på polär form.
Rättas inte automatiskt. Du bedömer själv mot facit.Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedöm ditt svarBedömningsanvisningar/Manuell rättningJämför med rätt svar ovan och kryssa i det du har fått med.Rätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Se mer:Videolektion: Komplexa tal på Polär formRättar...a-uppgifter (1)
-
12. Premium
Skriv talet $z=\sqrt{3}\left(\cos\frac{2\pi}{3}-i\sin\frac{2\pi}{3}\right)$z=√3(cos2π3 −isin2π3 ) på polär form.
Rättas inte automatiskt. Du bedömer själv mot facit.Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedöm ditt svarBedömningsanvisningar/Manuell rättningJämför med rätt svar ovan och kryssa i det du har fått med.Rätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Se mer:Videolektion: Komplexa tal på Polär formRättar... -
Din skolas prenumeration har gått ut!Din skolas prenumeration har gått ut! -
-
Uppgiften är en del av en abc-fråga. Vad vill du göra?
Det finns inga befintliga prov.
-
{[{ test.title }]}
●
Lektion
Kategori
ID
Test i 7 dagar för 9 kr.
Det finns många olika varianter av Lorem Ipsum, men majoriteten av dessa har ändrats på någotvis. Antingen med inslag av humor, eller med inlägg av ord som knappast ser trovärdiga ut.
Logga in
viaAll svar raderas. Detta går inte att ångra detta.
Kia Revo
Hej
Fråg 2 , hur har kommit till 6? längden på viktorn visar 4 och förstår inte vad är 3 för någonting. Den där frågan ser lite konstingt till mig behöver ännu mer förklaring
Eddler
Hej!
Absolutbeloppet (vektorns längd) beräknas med Pythagoras sats utifrån koordinaterna i det komplexa talplanet, inte genom att direkt avläsa linjelängden visuellt. Räknar man ut det från koordinaterna i bilden får man $|z| = 6$. Om det är svårt att se kopplingen, kolla gärna genomgångarna om komplexa tal på polär form!
Emil Ohlson
uppgift 10, hur vet man att den ligger i den fjärde kvadranten?
Sara Petrén Olauson
Hej! Realdelen av talet $z$ är positiv och imaginärdelen är negativ. Det innebär att det komplexa talet finns i den fjärde kvadranten. Skissa gärna det komplexa talplanet och jämför med Exempel 4. Hoppas att det hjälper dig vidare!
Sebastian cocha olsborg
Hur tar man reda på rad när man endast får vinkeln i grader som i uppgift 7 då 180-arctan(15/8)=129 grader
Sara Petrén Olauson
Hej! Om du väljer radianer i inställningarna på din räknare kan du direkt använda $v=\pi -\tan ^{-1}(\frac{15}{8})=2,06...\approx 2,1$ rad, istället för att gå via grader.
Men om du skulle ha en vinkel i grader kan du omvandla den till enheten radianer genom att använda faktorn $\frac{2\pi}{360^\circ}$. I detta fall skulle det innebära $v=180^{\circ }-\tan ^{-1}(\frac{15}{8})=118,07...^{\circ }$
I radianer får vi då: $118,07...^{\circ }\cdot \frac{2\pi }{360^{\circ }}=2,06...\approx 2,1$ rad.
Martin S
uppgift 6
hur ska man veta att vektorn ligger i fjärde kvadranten bara genom att titta på uppgiften?
tack på förhand
Per Eriksson
Hej,
Fråga 1 borde få "3pi/2" som korrekt svar? 🙂
Mvh Per
Wael Mahrous
Hej!
På exempel 2 i texten så står det först att r = 5, men sedan sätter ni roten ur 20 istället...
Tack för coola tjänsten!
Ludvig Johansson
angående fråga 2. borde inte svaret vara absolutbelopp 5? bilden är vilseledande.
Tacksam att denna tjänst finns.
IA
Hej.
Runt 4:43 borde inte a i absolut beloppet z bli -4^2? Har det någon betydelse om a och b. Alltså im och re är negativa när du ska räkna ut absolut beloppet?
IA
Tack så mycket!
bigr
Angående fråga 7:
Skriv z=−8+15i på polär form
FÖRKLARING
Vektorn för det komplexa talet ligger i andra kvadranten så argumentet beräknas enligt
v=180−arctan(15/12)≈129°
Det komplexa talet på polär form kan nu skrivas som
z=17(cos129°+isin129°)
-------------------
Varför divideras 15 med 12? Är det inte arctan(b/a), dvs. 15/8?
Sunshineklein
Väldigt klantig svenska där ser jag direkt :P. Så går det när man ivrigt pressar på "send".
Sunshineklein
Jag sjukt tacksam för dina videos. Läser ingenjör på högskola och fick även jag en smärre chock när jag insåg att ett matte D för 10 år sedan inte hjälpte långt när mattematiken snabbt blev tillämpad. Fortsätt med ditt goa arbete, det hjälper något så fantastiskt! Kommer säkert med någon fråga men än så länge är det sjukt illustrativt och pedagogiskt 🙂
lkhall
Det ser ut som att jag svart rätt men fått fel. Kanske Bör åtgärdas.
Låt z=4(cos(90°)+isin(90°)), skriv z på formen z=a+ib. Du svarade tyvärr fel
Ditt svar: z=4i
Rätt Svar: z=4i
Endast Premium-användare kan kommentera.