Författare: Simon Rybrand
Simon Rybrand
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Innehåll
De imaginära talen var en ny typ av tal, som utformades bland annat för att kunna hantera ekvationer där lösningen krävde att dra roten ur ett negativt tal. Med de imaginära talen och definitionen av $i^2=-1$i2=−1 ges just den möjligheten. Roten (lösningen) till en sådan ekvation är ett komplext tal.
Enkla ekvationer med komplexa rötter
Vissa ekvationer med komplexa rötter liknar de ”vanliga” andragradsekvationerna, och då kan roten ur, nollproduktmetoden eller pq-formeln användas. Det vi behöver komplettera metoderna med är att i2=−1i2=−1.
Exempel 1
Lös ekvationen x2−8x+25=0x2−8x+25=0 .
Lösning
Vi använder pq-formeln:
x2−8x+25=0x2−8x+25=0
x=4±16−25x=4±√16−25
x=4±−9x=4±√−9
x=4±3ix=4±3i
Ekvationens lösningar är
{x1=4+3ix2=4−3i
Ekvationer av typen zn=w
Det finns även ekvationer där både högerled och vänsterled består av komplexa tal. En strategi för att lösa dessa ekvationer är följande:
- Skriv om VLVL och HLHL på polär form
- Sätt leden lika med varandra och lös ut argumentet med periodicitet och absolutbeloppet.
- Använd argumentets periodicitet för att hitta alla lösningar till ekvationen.
Exempel 2
Lös ekvationen z4=iz4=i
Lösning
Eftersom ekvationen är en fjärdegradsekvation finns fyra möjliga lösningar. Vi börjar med att skriva om VLVL och HLHL till polär form för att sedan sätta dem lika med varandra och lösa ekvationen.
z=r(cosv+isinv)z=r(cosv+isinv)
VL=z4=r4(cos4v+isin4v)VL=z4=r4(cos4v+isin4v) enligt de Moivres formel
HL=i=0+iHL=i=0+i på rektangulär form, vilket ger absolutbeloppet:
∣0+i∣=02+12=1|0+i|=√02+12=1
Argumentet är 2ππ2 eftersom talet ii ligger på den positiva imaginära axeln i det komplexa talplanet.
Detta innebär att ii på polärform är 1(cos2π+i sin2π)1(cosπ2 +i sinπ2 ).
Likheten VL=HLVL=HL ger att:
r4(cos4v+i sin4v)=1(cos2π+i sin2π)r4(cos4v+i sin4v)=1(cosπ2 +i sinπ2 )
Det leder till
{r4=14v=2π+n⋅2π
Vi får
r4=1r4=1
r=1r=1
och kan bestämma vv genom
4v=2π+n⋅2π4v=π2 +n·2π
v=8π+n⋅2πv=π8 +n·π2
⇒⇒ z=cos(8π+n⋅2π)+i sin(8π+n⋅2π)z=cos(π8 +n·π2 )+i sin(π8 +n·π2 )
För att få de fyra olika lösningarna kan vi nu sätta n=0, 1, 2, 3n=0, 1, 2, 3 och förenkla ekvationen.
För n=0n=0 gäller
v1=8π+0⋅2π=8πv1=π8 +0·π2 =π8 som ger
z1=cos8π+i sin8πz1=cosπ8 +i sinπ8
För n=1n=1 gäller
v2=8π+1⋅2π=85πv2=π8 +1·π2 =5π8 som ger
z2=cos85π+i sin85πz2=cos5π8 +i sin5π8
För n=2n=2 gäller
v3=8π+2⋅2π=89πv3=π8 +2·π2 =9π8 som ger
z3=cos89π+i sin89πz3=cos9π8 +i sin9π8
För n=3n=3 gäller
v4=8π+3⋅2π=813πv4=π8 +3·π2 =13π8 som ger
z4=cos813π+i sin813πz4=cos13π8 +i sin13π8
De fyra lösningarna till ekvationen z4=iz4=i är
⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧z1=cos8π+isin8πz2=cos85π+isin85πz3=cos89π+isin89πz4=cos813π+isin813π
Beräknar vi vinkeln för n=4n=4 kommer den att sammanfalla med 8ππ8 eftersom att 817π=816π+8π=8π+17π8 =16π8 +π8 =π8 +2π2π , dvs vinkeln på nästa varv. Eftersom det ger samma komplexa rot som z1z1 behöver vi inte ange det som en lösning till ekvationen.
Grafisk tolkning av rötterna
I exemplet ovan ser vi att rötterna hamnar på en cirkel med medelpunkten i origo och radien 11, vilket motsvarar absolutbeloppet av ii.
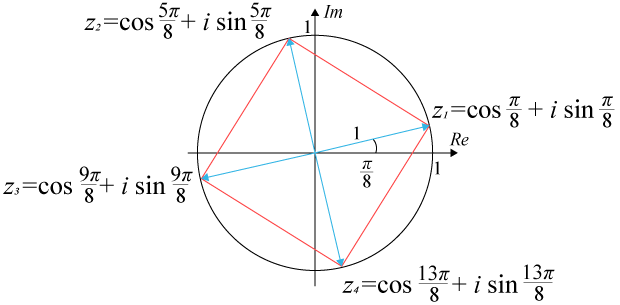
Mönstret att rötterna fördelar sig symmetriskt som punkter på en cirkel är återkommande när vi löser ekvationer på formen zn=wzn=w där nn är ett positivt helt tal och ww ett komplext tal. Vi kan sammanfatta det på följande vis:
Lösningarna till ekvationen zn=wzn=w i det komplexa talplanet utgör hörn i en regelbunden nn-hörning med medelpunkten i origo.
Exempel i videon
- Lös ekvationen x2=−16.
- Lös ekvationen x2+4x+13=0.
- Lös ekvationen z4=16i.
- Lös ekvationen z3=1.
Kommentarer
e-uppgifter (5)
1.
(1/0/0)E C A B P 1 PL M R K Lös ekvationen z2=−81z2=−81 .
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...2.
(1/0/0)E C A B P 1 PL M R K Lös ekvationen −1000−10x2=0−1000−10x2=0.
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...3.
(1/0/0)ME C A B P 1 PL M R K Lös ekvationen (3−x)2=−4(3−x)2=−4 .
Svar:Ditt svar:Rätt svar: x1=3+2i och x2=3−2i(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...4. Premium
(1/0/0)E C A B P 1 PL M R K Lös ekvationen z2+2z+2=0z2+2z+2=0 .
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...5. Premium
(1/0/0)M NPE C A B 1 P PL M R K z1=cos35∘+isin35∘z1=cos35∘+isin35∘ är en rot till ekvationen z9=wz9=w.
Bestäm en annan rot till samma ekvation.Svar:Ditt svar:Rätt svar: T ex cosz2=75∘+isin75°(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
c-uppgifter (3)
6. Premium
(0/1/0)ME C A B 1 P PL M R K Ange en icke-reell rot till ekvationen z6−3=0z6−3=0 .
Svar:Ditt svar:Rätt svar: T ex 63⋅(cos3π+isin3π)(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...7. Premium
(0/2/0)ME C A B P 2 PL M R K Lös ekvationen z3=27iz3=27i . Svara på rektangulär form.
Svar:Ditt svar:Rätt svar: ⎩⎪⎪⎨⎪⎪⎧z1=233+23iz2=−233+23iz3=−3i(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...8. Premium
(0/2/0)ME C A B P 2 PL M R K Lös ekvationen z5=−32iz5=−32i. Svara på polär form.
Svar:Ditt svar:Rätt svar: zn=2(cos(103π+n⋅52π)+i sin(103π+n⋅52π)) där n=0,1,2,3,4(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
a-uppgifter (1)
9. Premium
(0/0/3)M NPE C A B P 2 PL M R K 1 Lös ekvationen ∣z∣2=5z−10i|z|2=5z−10i
(Uppgift från nationella provet i Ma4 ht 2015.)
Svar:Ditt svar:Rätt svar: {z1=4+2iz2=1+2i(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Eddler
POPULÄRA KURSER
FÖRETAGSINFO
Eddler AB
info@eddler.se
Org.nr: 559029-8195
Kungsladugårdsgatan 86
414 76 Göteborg

rahand shaker
Hej!
Lyckas inte förstå var periodicitet kommer ifrån?
Johan Schmidt
Är det ett krav att man ska förenkla svaren till bråk? Min miniräknare ger mig endast decimalform så det känns som att det blir mer exakt att bara svara i polär form.
Daniel Öhman
Hur kommer man fram till argumentet? Har tittat igenom alla video tills denna och verkar inte kunna hitta svaret.
Simon Rybrand (Moderator)
Hej
Kolla här: https://eddler.se/lektioner/komplexa-tal-pa-polar-form/
Jacob Nilsson
Skriv z = 1−i √3 på polär form, bestäm sedan z^11 på rektangulär form (a+i b ).
Här undrar jag om argumentet ska vara -pi/3 eller 2pi/3? Jag har fått lära mig att jag ska addera ett pi om argumentet blir negativt. Sedan när jag ska bestämma z^11 så får jag inte riktigt till det
Simon Rybrand (Moderator)
Du har absolutbeloppet
12+(3)2=4=2
Gällande argumentet så kika på den här videon om komplexa tal på polär form, där förklarar vi hur man tänker kring detta. Men kortfattat så finns talet i fjärde kvadranten och då får vi
v=2π–arctan(3)
Hoppas att det här hjälper dig vidare!
Karl Tellander
Mitt tal: z^2+2z+2= 0 Blir med hjälp av pq formerln.
-1 +/- roten ur -1.
Hur bryter jag ur i ur -1?
i = \sqrt{-1}
Simon Rybrand (Moderator)
Här har vi ju
z2+2z+2=0⇔
z=−1±1−2
z=−1±−1
Här gäller att −1=i så du kan svara
z=−1±i
Du behöver inte ”bryta ut” -1 där utan det räcker med att använda dig av imaginära tal för att kunna svara.
Du kan även ange bägge rötterna som
{z1=−1+iz2=−1−i
soulpat
ekvationen z^5=-32 är given.
Skriv om ekvationen i polär form:
Mitt förslag: r^5(cos5v+isin5v)=32(cos0+isin0)
Facit: r^5(cos5v+isin5v)=32(cos(180+360*n)+isin(180+360*n))
Vart får man 180 grader ifrån? Jag får det till 0.
soulpat
Tror jag förstår nu!
Simon Rybrand (Moderator)
Vad bra, skönt att läsa!
Endast Premium-användare kan kommentera.