Författare: Simon Rybrand
Simon Rybrand  Anna Karp
Anna Karp
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Innehåll
Denna lektion är en repetition av derivata och de deriveringsregler vi lärt oss i tidigare kurser.
Repetition av Derivata
Derivata är en funktion som anger förändringshastigheten hos en annan känd funktion. Funktionens derivata beskriver hur mycket och i vilken riktning funktionens värde förändras då man rör sig från en given punkt.

Inom matematiken är beräkningar av derivatan en metod att studera och beräkna funktioners förändringar.
Återvänd till lektionen för repetition Derivata – Vad är det? om du vill veta mer.
Derivatan – ett gränsvärde
Vi börjar denna repetition av derivata med definitionen.
Den genomsnittliga förändringshastigheten över ett intervall kan beräknas med en ändringskvot. Ändringskvoten motsvarar sekants lutning i intervallet. Derivatan definieras som gränsvärdet till denna ändringskvot.
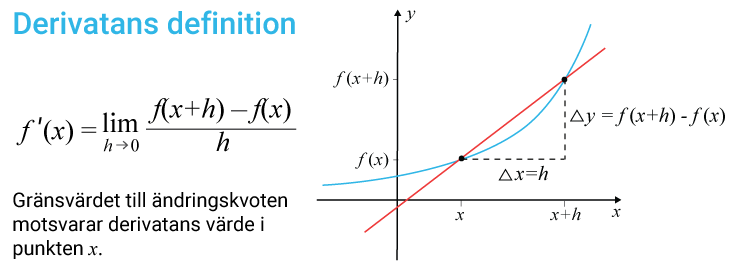
Derivatan i en punkt kan alltså beräknas med hjälp av gränsvärdet av ändringskvoten där en sekant går till att bli en tangent till kurvan. Omvandlingen från sekant till tangent sker då avståndet mellan punkterna där sekanten skär genom grafen, går mot noll. Alltså i gränslandet där de två punkterna sammanfaller.
Derivatans definition
f′(x)=h→0lim hf(x+h)−f(x)ƒ (x+h)−ƒ (x)h
Återvänd till lektionen för repetition Derivatans definition om du vill veta mer.
Så betecknas Derivata
En funktion betecknas med matematiskt språk oftast med f(x)ƒ (x) eller yy. För att beskriva derivatan till f(x)ƒ (x) använder man vanligtvis beteckningen f’(x)ƒ ’(x). Det uttalar man som ”f prim av x”. Men det finns fler sätt att beteckna derivata. Här är några.
y’y’ y’(x)y’(x) dxdydydx dxdfdƒ dx Df(x)Dƒ (x) DyDy
Deriveringsregler
Innan vi tittar på de olika funktionernas deriveringsregler gör vi denna repetition av derivata.
Tre bra kom ihåg när du deriverar
- Du deriverar alltid ett uttryck ”term för term”.
- Derivatan av en konstant är alltid lika med noll.
- Derivatan av en förstagradsterm är alltid lika med koefficienten.
Här samlar vi de deriveringsregler vi lärt oss i tidigare kurs.
Polynomfunktioner och Potensfunktioner
Vid derivering av polynomfunktioner och potensfunktioner gäller följande.

En polynomfunktion är ju en särskild sorts protesfunktion där alla exponenter tillhör de naturliga talen. Det leder till att samma deriveringsregel gäller för både polynomfunktioner och potensfunktioner.
En funktion f(x)=kxnƒ (x)=kxn, där kk är en konstant har derivatan
f′(x)=n⋅k⋅xn−1ƒ ´(x)=n·k·xn−1
För alla funktioner f(x)=k⋅g(x)ƒ (x)=k·g(x) där kk är en konstant, gäller att f′(x)=k⋅g′(x)ƒ ´(x)=k·g´(x)
Eftersom att en polynom- och potensfunktioner kan ha flera termer använder vi följande regler för att kunna derivera dem.
D(f+g)=f′+g′D(ƒ +g)=ƒ ´+g´
Exempel på att derivera polynomfunktioner
y=x har derivatan y′=1
f(x)=x3 har derivatan f′(x)=3x2
g(x)=2x4+3x+10 har derivatan g′(x)=8x3+3+0=8x3+3
Lektion om att derivera polynomfunktioner
En potensfunktion kan innehålla andra exponenter än positiva heltal, exempelvis bråktal eller negativa tal. För potensfunktioner används ändå samma deriveringsregler som för polynomfunktioner.
Potensregler som underlättar derivering
1) a−n=a−n= an11an
2) nx=x1/nn√x=x1/n
Exempel på att derivera potensfunktioner
f(x)=x=x1/2 har derivatan f′(x)=21x−1/2=2x1
y=x21=x−2 har derivatan y′=−2x−3=x3−2
Lektion om att derivera potensfunktioner
Exponentialfunktioner
För funktioner som har sin oberoende variabel i exponenten gäller följande deriveringsregel.

f(x)=Cakxƒ (x)=Cakx där a>0a>0 har derivatan f′(x)=Cakx⋅k⋅lnaƒ ´(x)=Cakx·k·lna
Eftersom att lne=1lne=1 blir derivatan ännu enklare för exponentialfunktioner med basen e.
f(x)=Cekxƒ (x)=Cekx har derivatan f′(x)=Cekx⋅kƒ ´(x)=Cekx·k
Exempel på att derivera exponentialfunktioner
f(x)=ex har derivatan f′(x)=ex
g(x)=2e3x har derivatan g′(x)=6e3x
y=2x har derivatan y′=2x⋅ln2y´=2x·ln2
Andraderivata – derivatans derivata
När man deriverar en derivata, får man något som man kallar för andraderivatan. Den betecknar man på många olika sätt. Några ser du här.
y′′ f′′(x) dx2d2yd2ydx2
Skrivsättet ′′ uttalar man som ”bis”.
Andraderivatan motsvarar förändringshastigheten av förändringshastigheten. Det innebär att man får andraderivatan till en funktion genom att man deriverar funktionen två gånger efter varandra.
Den huvudsakliga användningen av andraderivatan i denna kurs, är att vi med den mycket effektivt kan bestämma extrempunkternas karaktär, samt eventuella inflexionspunkter. Vi kan med andraderivatans hjälp även undersöka hur en graf ser ut och beter sig för olika xx -värden.

Återvänd till lektionen för repetition Andraderivatan om du vill veta mer.
Numerisk derivering och digitala verktyg
Tänk på att utnyttja digitala hjälpmedel när du får. De kan effektivisera beräkningar och underlätta svåra deriveringar.
Dessutom är det nödvändiga vid derivering av vissa funktioner, tex y=5x3⋅cos2x⋅4xy=5x3·cos2x·4x.
Exempel i videon
Kommentarer
e-uppgifter (13)
1.
(1/0/0)E C A B P 1 PL M R K Derivera f(x)=3x+2ƒ (x)=3x+2
Svar:Ditt svar:Rätt svar: f′(x)=3(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Förkunskap: Deriveringsregler PolynomfunktionerRättar...2.
(1/0/0)E C A B P 1 PL M R K Derivera f(x)=x3ƒ (x)=x3
Svar:Ditt svar:Rätt svar: f′(x)=3x2(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Förkunskap: Deriveringsregler PolynomfunktionerRättar...3.
(1/0/0)E C A B P 1 PL M R K Derivera f(x)=7xƒ (x)=7x
Svar:Ditt svar:Rätt svar: f′(x)=7(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Förkunskap: Deriveringsregler PolynomfunktionerRättar...4. Premium
(1/0/0)E C A B P 1 PL M R K Derivera f(x)=82ƒ (x)=82
Svar:Ditt svar:Rätt svar: f′(x)=0(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Förkunskap: Deriveringsregler PolynomfunktionerRättar...5. Premium
(1/0/0)E C A B P 1 PL M R K Derivera f(x)=5e2xƒ (x)=5e2x
Svar:Ditt svar:Rätt svar: f′(x)=10e2x(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Förkunskap: Deriveringsregler ExponentialfunktionerRättar...6. Premium
(1/0/0)E C A B P 1 PL M R K Låt f(x)=3x3+2x2−10x+4ƒ (x)=3x3+2x2−10x+4 . Bestäm f′(x)ƒ ´(x).
Svar:Ditt svar:Rätt svar: f′(x)=9x2+4x−10(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Förkunskap: Deriveringsregler PolynomfunktionerRättar...7. Premium
(2/0/0)M NPE C A B P 2 PL M R K Olle och Olga säljer kantareller och funderar på att höja kantarellernas kilopris för att öka dagsinkomsten. De har kommit fram till att dagsinkomsten som funktion av prishöjningen ges av
f(x)=−0,1x2+5x+3000ƒ (x)=−0,1x2+5x+3000
där f(x)ƒ (x) dagsinkomsten i kr och xx är prishöjningen i kr/kg.

Beräkna, med hjälp av derivata, vilken prishöjning xx som ger den största dagsinkomsten.
Svar:Ditt svar:Rätt svar: 25 kr/kg(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...8. Premium
(1/0/0)E C A B P 1 PL M R K Derivera f(x)=ƒ (x)= x355x3
Svar:Ditt svar:Rätt svar: f′(x)=−x415(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Förkunskap: Deriveringsregler PotensfunktionerRättar...9. Premium
(1/0/0)E C A B P 1 PL M R K Derivera f(x)=4xƒ (x)=4√x och förenkla.
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...10. Premium
(1/0/0)E C A B P 1 PL M R K Bestäm andraderivatan till f(x)=4x3+3x2ƒ (x)=4x3+3x2
Svar:Ditt svar:Rätt svar: f′′(x)=24x+6(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...11. Premium
(1/0/0)E C A B P 1 PL M R K Bestäm dtdVdVdt om V(t)=3πt2V(t)=3πt2
Svar:Ditt svar:Rätt svar: dtdV=6πt(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...12. Premium
(1/0/0)E C A B P 1 PL M R K Bestäm dt2d2Vd2Vdt2 om V(t)=3πt2V(t)=3πt2
Svar:Ditt svar:Rätt svar: dt2d2V=6π(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...13. Premium
(1/0/0)E C A B P 1 PL M R K Låt f(x)=2x4−x2+12x+exƒ (x)=2x4−x2+12x+ex. Bestäm f′′(x)ƒ ´´(x).
Bedömningsanvisningar/Manuell rättning- Rättad
Förkunskap: AndraderivataRättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
c-uppgifter (9)
14. Premium
(0/1/0)E C A B P 1 PL M R K Bestäm f′(x)ƒ ’(x) om f(x)=−ƒ (x)=−x22√x
Svar:Ditt svar:Rätt svar: f′(x)=x31(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...15. Premium
(1/1/0)E C A B 1 P PL M R 1 K Vilken av graferna nedan skulle kunna vara den ursprungliga funktionen f(x)ƒ (x) då dess andraderivata är f′′(x)=6x+2ƒ ´´(x)=6x+2
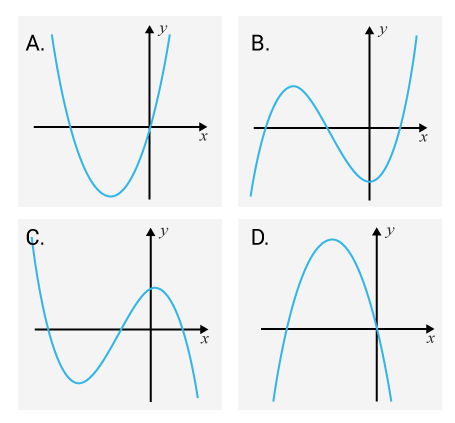
Motivera ditt val för att få poäng för resonemang.
Svar:Ditt svar:Rätt svar: Graf B.(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Se mer: AndraderivataRättar...16. Premium
(0/2/0)E C A B P 2 PL M R K Bestäm f′′(9)ƒ ´´(9) om f(x)=ƒ (x)= 23x3√x2
Ange svaret på enklaste form.
Svar:Ditt svar:Rätt svar: f′′(x)=−721(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Förkunskap: AndraderivataRättar...17. Premium
(3/4/0)M NPE C A B 2 P PL M 3 2 R K Temperaturen hos vattnet i en flaska som ställs in i ett kylskåp kan beskrivas med modellen T(x)=17e−0,693x+5T(x)=17e−0,693x+5 där T(x)T(x) är vattnets temperatur i °C°C och xx är tiden i timmar efter att flaskan ställdes in i kylskåpet.
a) Bestäm vattnets temperatur då flaskan ställs in i kylskåpet.
b) Bestäm efter hur lång tid vattnets temperatur är 10 °C10 °C.
c) Bestäm hur snabbt vattnets temperatur sjunker två timmar efter att flaskan ställdes in i kylskåpet.
d) Enligt modellen kommer vattnets temperatur med tiden att närma sig en undre gräns. Bestäm denna undre gräns med hjälp av modellen.
Svar:Ditt svar:Rätt svar: a) 22° C b) 1,8 h c) 2,9 °C/h d) 5°C(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Se mer: Problemlösning med DerivataRättar...18. Premium
(0/2/0)E C A B P PL 2 M R K Grafen till f(x)=x5−5x2ƒ (x)=x5−5x2 har en tangent i punkten PP som ligger i tredje kvadranten.
Tangenten har lutningen 1515. Bestäm xx-koordinaten för punkten PP.
Svar:Ditt svar:Rätt svar: x=−1(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Se mer: Tangentens ekvation och lutningRättar...19. Premium
(0/2/0)ME C A B P PL 2 M R K Bestäm en andragradsfunktion fƒsom uppfyller villkoret att f′(4)=5ƒ ´(4)=5
Svar:Ditt svar:Rätt svar: Tex en variant av f(x)=x2−3x+c, tex f(x)=x2−3x(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...20. Premium
(0/1/0)E C A B P 1 PL M R K Bestäm f′(x)ƒ ’(x) om f(x)=ƒ (x)=28x+2e−x8x+2e−x2
Svar:Ditt svar:Rätt svar: f′(x)=4−e−x(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...21. Premium
(0/2/0)E C A B P 2 PL M R K Beräkna f′(x)ƒ ´(x) då f(x)=4⋅22x−ƒ (x)=4·22x−x24√4x2
Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...22. Premium
(0/2/1)ME C A B 1 P 1 PL M R K 1 Bestäm f′(x)ƒ ´(x) med hjälp av derivatans definition då f(x)=x2+3xƒ (x)=x2+3x.
Svar:Ditt svar:Rätt svar: Se förkaring.(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Förkunskap: Exempel derivatans definitionRättar...
a-uppgifter (6)
23. Premium
(0/1/2)E C A B P 1 PL 1 M R 1 K 
Antalet lämlar N(t)N(t) i en lämmelkoloni kunde beskrivas med funktionen N(t)=3t(t−3)(t−5)+400N(t)=3t(t−3)(t−5)+400 då 0≤t≤80≤t≤8 motsvarar antal år efter 20082008.
Vilket år ökade kolonin med ca 8080 lämlar/år?
Svar:Ditt svar:Rätt svar: År 2014.(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...24. Premium
(0/1/1)NPE C A B 1 1 P PL M R K Ange alla funktioner som har egenskapen att f(x)=f′(x)ƒ (x)=ƒ ´(x) där f(x)=0ƒ (x)≠0.
Svar:Ditt svar:Rätt svar: y=ex(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Rättar...25. Premium
(0/0/1)E C A B P PL M R 1 K Visa att f′(x)=8x⋅ln8ƒ ’(x)=8x·ln8 då f(x)=ƒ (x)= 2−3x112−3x
Svar:Ditt svar:Rätt svar: Se förklaring.(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Förkunskap: Deriveringsregler ExponentialfunktionerRättar...26. Premium
(0/0/2)M NPE C A B P PL 2 M R K Albins vikt kan beskrivas med funktionen V(t)=0,10t3−1,23t2+6,51t+3,72V(t)=0,10t3−1,23t2+6,51t+3,72 där vikten VV kg är en funktion av tiden tt år efter födseln. Funktionen gäller under hans åtta första levnadsår.

Den hastighet som Albins vikt ökar med varierar. Bestäm vilka värden hastigheten kan anta under Albins åtta första levnadsår.
Svar:Ditt svar:Rätt svar: 1,5≤V′(t)≤6,5(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Förkunskap: Minsta och Största värde AndraderivataRättar...27. Premium
(0/1/2)ME C A B 1 1 P PL M R K 1 Bestäm f′(x)ƒ ´(x) med hjälp av derivatans definition då f(x)=ƒ (x)=x11x
Svar:Ditt svar:Rätt svar: Se förklaring.(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Förkunskap: Exempel derivatans definition Derivatans DefinitionRättar...28. Premium
(0/0/3)ME C A B P PL 1 M 1 R 1 K 
Din vän häller upp en kopp te för att värma sig lite. Temperaturen i luften där din vän befinner sig är 1818 °C. Hon mäter temperaturen på teet i koppen direkt när hon häller i det och sedan igen efter 55 minuter.
Hon tänker teckna en matematisk modell från sina mätvärden. Hon bestämmer sig för en exponentialfunktion.
Hon sätter T(t)T(t) till teets temperatur i °C och tt till tiden i minuter efter att det hälldes upp i koppen. Temperaturen var 8080 °C vid första mätningen och 6161 °C vid andra mätningen.
Bestäm och tolka T’(3)T’(3) samt ange huruvida du anser den matematiska modellen vara rimlig eller ej.
Svar:Ditt svar:Rätt svar: Se förklaring.(Korrekta varianter)Bedömningsanvisningar/Manuell rättning- Rättad
Förkunskap: Problemlösning med DerivataRättar...
Allt du behöver för att klara av nationella provet
Allt du behöver för att klara av nationella provet
Eddler
POPULÄRA KURSER
FÖRETAGSINFO
Eddler AB
info@eddler.se
Org.nr: 559029-8195
Kungsladugårdsgatan 86
414 76 Göteborg

Leon Stenberg Wadstrom
Hej,
Denna sida har varit jättehjälpsam, bara en snabb fråga. På uppgift 8 i förklaring så står det att -h/x(x+h) gånger 1/h blir -1/x(x+h).
Jag förstår inte riktigt hur -h gånger 1 blir -1 och hur h gånger x(x+h) blir x(x+h)
Tack så mycket för hjälpen.
Leon
holm.nathalie
Hej!
Om man har f prim dvs. f ’ (y) = roten ur y så kommer jag så långt att:
roten ur y är samma sak som y^1/2
sen måste man plussa på 1
y = y^1+ 1/2 = y^3/2
men sen då?? Tar jag ned 3/2 framför y och delar med 3/2 så tar ju de ut varandra?
Tacksam för svar 🙂
Simon Rybrand (Moderator)
Svarar gärna men vilken uppgift är det som du jobbar med?
Någon från övningarna här eller någon annanstans? Kan du skriva ned frågan här?
RasmusP
Nu är det något fel med alla tecken. Det står $ osv istället för talen på frågorna.
”
Vad är derivatan av x3x3?
x^3$
$
x2x2
x^2$
FÖRKLARING
I formelsamlingen kan vi se att derivatan av xaxa är a⋅xa−1a⋅xa−1.
Tillämpat på frågan får vi att derivatan av x3x3 är:
\cdot x^{3-1} = 3x^2$
”
Simon Rybrand (Moderator)
Hej
Detta kan bero på att du har javascript (programmeringsspråket som gör om formlerna) avstängt i din webbläsare. Testa gärna med en annan webbläsare och hör av dig om det fortfarande inte fungerar!
Jonathan Sundström
Fråga 4 verkar inte stämma, derivatan av sin(x) ska väl vara cos(x) och inte cos2(x) som den rättar som rätt svar.
Simon Rybrand (Moderator)
Hej, tänk på att du här måste använda dig av produktregeln. Derivatan av sin(x) är cos(x) men eftersom du inte deriverar cos(x) så får du cos(x)⋅cos(x)=cos2x
Mikael
Fråga fyra har två likadana alternativ 1 och 3.
Simon Rybrand (Moderator)
Hej och tack för kommentaren, det är korrigerat i testet.
Leila
Hej!
Jag svarade rätt på alla frågor men det visas 80% rätt!
Det inte stämmer.
Hälsningar
Leila
Simon Rybrand (Moderator)
Hej, vilken fråga är det som du får fel på?
Endast Premium-användare kan kommentera.