Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Matematik 1c
/ Trigonometri och Vektorer
Enkla Trigonometriska ekvationer
I en tidigare lektion lärde vi oss hur man med hjälp av de trigonometriska funktioner kunde bestämma rätvinkliga trianglars sidlängder och vinklar. Vi ska nu lösa trigonometriska ekvationer med hjälp av den kunskapen.
Bestäm vinkeln med inversen
För att kunna lösa trigonometriska ekvationer behöver man känna till begreppet nedan.
$\sin⁻¹$ eller $ \arcsin$ vilket är två olika skrivsätt för sinusinvers.
$\cos⁻¹ $ eller $\arccos$ vilket är två olika skrivsätt för cosinusinvers.
$\tan⁻¹ $ eller $ \arctan$ vilket är två olika skrivsätt för tangensinvers.
För trigonometriska ekvationer är metoden att med hjälp av inversen få $x$x ensamt i ena ledet. På din räknare brukar du oftast hitta inversen skriven som sin⁻¹, cos⁻¹ och tan⁻¹. Vanligt är att du trycker knappen $2nd$2nd och sedan knappen för den trigonometriska funktionen för att komma åt dessa funktioner.
Kontrollera att din räknare är inställd på grader och inte radianer. Annars kommer du få fel svar på uppgifterna.
Vi kommer i senare kurser jobba med vinkelmåttet radianer. Men i denna kurs håller vi oss till grader.
Exempel trigonometrisk ekvation Premium
Exempel 1
Lös ekvationen $\sin x=0,95$sinx=0,95
Lösning
Vi löser uppgiften men hjälp av räknarens inversfunktion.
$\sin x=0,95$sinx=0,95
$\sin^{-1}(\sin x)=\sin^{-1}(0,95)$sin−1(sinx)=sin−1(0,95)
Slå in $\sin^{-1}\left(0,95\right)$sin−1(0,95) eller $\arcsin\left(0,95\right)$arcsin(0,95) som är två namn på samma sak. Vi får att
$ x \approx 72^{\circ} $
Men ekvationen kan vara mer invecklade än så.
Exempel 2
Lös ekvationen $4+\cos x=4,5$4+cosx=4,5
Lösning
Vi löser uppgiften men hjälp av räknarens inversfunktion efter att vi har skrivit om uttrycket så att den trigonometriska termen är ensam i ena ledet.
$4+\cos x=4,5$4+cosx=4,5 subtrahera båda leden med $4$4
$\cos x=0,5$cosx=0,5
Slå in $\cos^{-1}\left(0,5\right)$cos−1(0,5) eller $\text{arccos}\left(0,5\right)$arccos(0,5) som är två namn på samma sak, på din räknare. Vi får att
$x=60^{\circ}$x=60∘
Exempel i videon Premium
- Beräkna $\sin55°$sin55° .
- Beräkna $\sin^{-1}(0,819)$sin−1(0,819) .
- Lös ekvationen $\sin x=0,62$sinx=0,62 .
- Bestäm längden på sidan $x$x i en rätvinklig triangel där en vinkel och en annan sida är angiven.
Kommentarer
██████████████████████████
████████████████████████████████████████████████████
e-uppgifter (8)
-
1. Premium
Rapportera fel Ändra till korrekt (1/0/0)M NPE C A B P 1 PL M R K Lös ekvationen $\sin x=$sinx=$\frac{1}{2}$12
Bedömningsanvisningar/Manuell rättning-
-
Rättad
-
+1
-
Rättad
Rättar... -
2. Premium
Rapportera fel Ändra till korrekt (1/0/0)M NPE C A B P PL M R 1 K Vilket av följande påstående är rätt?
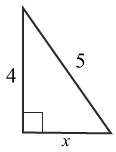Bedömningsanvisningar/Manuell rättning-
-
Rättad
-
+1
-
Rättad
Rättar... -
3. Premium
Rapportera fel Ändra till korrekt (1/0/0)M NPE C A B 1 P PL M R K Vilken är motstående sida till vinkeln v?
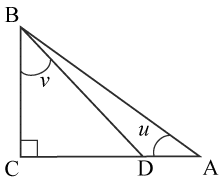Bedömningsanvisningar/Manuell rättning-
-
Rättad
-
+1
-
Rättad
Rättar... -
4. Premium
Rapportera fel Ändra till korrekt (1/0/0)M NPE C A B P 1 PL M R K Lös ekvationen $\cos\left(x\right)=$cos(x)=$\frac{3}{4}$34
Bedömningsanvisningar/Manuell rättning-
-
Rättad
-
+1
-
Rättad
Rättar... -
5. Premium
Rapportera fel Ändra till korrekt (1/0/0)M NPE C A B P 1 PL M R K Beräkna vinkeln v i triangeln.
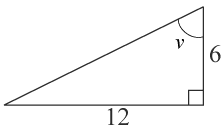Bedömningsanvisningar/Manuell rättning-
-
Rättad
-
+1
-
Rättad
Rättar... -
6. Premium
Rapportera fel Ändra till korrekt (1/0/0)M NPE C A B P 1 PL M R K Lös ekvationen $\tan x-$tanx− $\frac{1}{5}$15 $=0$=0
Bedömningsanvisningar/Manuell rättning-
-
Rättad
-
+1
-
Rättad
Rättar... -
7. Premium
Rapportera fel Ändra till korrekt (2/0/0)M NPE C A B P PL 1 M R 1 K Bestäm den minsta vinkeln i en rätvinklig triangel där kateternas längder är $18$18 cm och $34$34 cm.
Bedömningsanvisningar/Manuell rättning-
-
Rättad
-
+1
-
Rättad
Rättar... -
8. Premium
Rapportera fel Ändra till korrekt (1/0/0)M NPE C A B P 1 PL M R K En rätvinklig triangel har en vinkel $42$42 ° vars närliggande katet är $3$3 cm.
Beräkna längden på hypotenusan.
Bedömningsanvisningar/Manuell rättning-
-
Rättad
-
+1
-
Rättad
Rättar...
c-uppgifter (2)
-
9. Premium
Rapportera fel Ändra till korrekt (1/1/0)M NPE C A B P PL M R 1 1 K Bestäm den största vinkeln i en rätvinklig triangel där kateten är $12$12 cm och hypotenusan är $13$13 cm.
Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättning-
-
Rättad
-
+1
-
Rättad
Rättar...10. Premium
Rapportera fel Ändra till korrekt (0/4/0)M NPE C A B 1 P 1 PL 2 M R K Bestäm triangelns omkrets då $\tan x=1$tanx=1 och den längsta sidan på triangeln är $\sqrt{8}$√8 l.e.
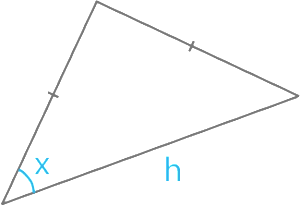Svar:Ditt svar:Rätt svar:(Korrekta varianter)Ger rätt svar {[{correctAnswer}]}Bedömningsanvisningar/Manuell rättning-
-
Rättad
-
+1
-
Rättad
Rättar... -
Det finns inga befintliga prov.
-
{[{ test.title }]}
●
Lektion
Kategori
ID
Test i 7 dagar för 9 kr.
Det finns många olika varianter av Lorem Ipsum, men majoriteten av dessa har ändrats på någotvis. Antingen med inslag av humor, eller med inlägg av ord som knappast ser trovärdiga ut.
Logga in
viaAll svar raderas. Detta går inte att ångra detta.
Dorota Nilsson
Hej, titta på uppg 3. Svar: sidan CD finns 2 ggr.
Simon Rybrand (Moderator)
Fixat! Tack!
Daniel Lövquist
Hej
I fråga 6 så har jag valt svar v = 63,4grader men jag får ändå fel på den. Det står i förklaringen till frågan att svaret är v = 63,4grader.
Mvh Daniel
Simon Rybrand (Moderator)
Hej
Det var en bugg i den uppgiften, det är korrigerat, tack för att du sade till!
David Ahlstrom
Om man kollar formelbladet för nationellt prov. Dessa trigonometri formler stämmer ju inte om vi har graden v på andra sidan av hypotenusan (alltså ovanför istället för vid sidan om). Den formelgrupp som ni har skrivit här stämmer ju.
sinv=motstående katet/hypotenusa
cosv=närliggande katet/hypotenusa
tanv=motstående katet/närliggande katet
Men varför har dom en felaktig formelsamling? Den visar ju bara rätt när graden är på ett ställe.
Tänkte att man kan få fram den rätta graden genom att ta den grad man har + 90 och sen ta 180 minus den summan. Men det blev fel i uträkningen ändå. Tex förra kapitlet fråga 7.
Tack för svar.
Mvh David
Ida Comstedt Centerlid
Om x är på hypotenusan, hur räknar jag då?
Simon Rybrand (Moderator)
Det beror på vad du känner till mer, närliggande eller motstående kateten?
mcnewbie
Hej,
Jag förstår inte förklaringen av sista uppgiften. Från att vara 0,74x = 3 till att x = 4,05
Simon Rybrand (Moderator)
Det som händer där är att vi dividerar både vänsterledet och högerledet med 0,74 för att få x ensamt, dvs:
$ 0,74x = 3 $ (dividera med 0,74)
$ \frac{0,74x}{0,74} = \frac{3}{0,74} $
$ x = 4,05 $ (Avrundat)
Pedro Veenekamp
Hej!
Skulle det inte avrundas till 4,04 istället? Lösningen är nämligen 4,036898189…
Simon Rybrand (Moderator)
Hej
Jo det är egentligen bättre, viktigt är då att man först löser ut x och sedan beräknar $\frac{3}{cos(42)}$. Vi ändrar i den övningsuppgiften och visar detta.
Endast Premium-användare kan kommentera.