00:00
00:00
KURSER  / 
Matematik Högstadiet
/  Bråk och Bråkräkning
AritmetikBråk

Minsta gemensamma nämnare (MGN)

Författare:Simon Rybrand
PROVA GRATIS
Så hjälper Eddler dig:
Videor som är lätta att förstå Övningar & prov med förklaringar
Allt du behöver för att klara av nationella provet
PROVA GRATIS
Så hjälper Eddler dig:
Videor som är lätta att förstå Övningar & prov med förklaringar
Allt du behöver för att klara av nationella provet

Innehåll

Den minsta gemensamma nämnaren motsvarar det minsta tal som är delbart med alla nämnarna på bråktalen i ett uttryck samtidigt. Det innebär att minsta gemensamma nämnare är en multipel bråktalens nämnare. Minsta gemensamma nämnare förkortas ofta för MGN.

Du använder MGN för att kunna addera och subtrahera bråktal som står skrivna på olika nämnare.

Hitta den minsta gemensamma nämnaren

Den minsta gemensamma nämnaren

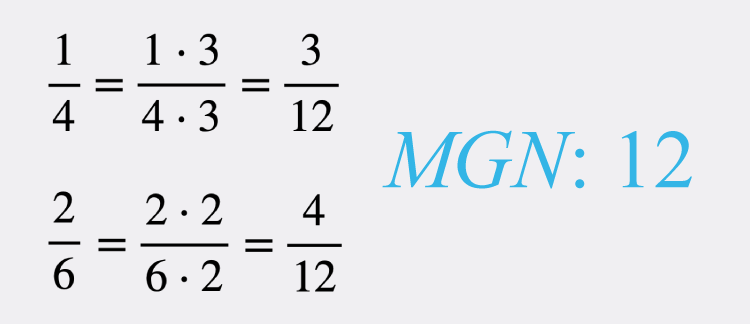
När du skall hitta den minsta gemensamma nämnaren så letar du efter det minsta heltal som du kan dela alla nämnare i bråken i uttryckt med.

För att förstå hur det går till så tar vi ett exempel med bråktalen 13\frac{1}{3}13  och 25\frac{2}{5}25 . Vi gör så att vi förlänger de bägge bråktalen med 2,3, 42,3,\text{ }42,3, 4 och 555 för att hitta en nämnare som är gemensam. Känner du dig osäker på hur du förlänger och förkortar kan du träna på det här.

 Urspungsbråk Förlängt med  222  Förlängt med  333  Förlängt med  444  Förlängt med  555 
 13\frac{1}{3}13    26\frac{2}{6}26    39\frac{3}{9}39    412\frac{4}{12}412    515\frac{5}{15}515  
 25\frac{2}{5}25    410\frac{4}{10}410    615\frac{6}{15}615    820\frac{8}{20}820    1025\frac{10}{25}1025  

Vi ser att den minsta gemensamma nämnaren är 151515. Den får vi när vi förlänger 13\frac{1}{3}13  med 555, det vill säga 1⋅53⋅5=515\frac{1\cdot5}{3\cdot5}=\frac{5}{15}1·53·5 =515   

och  25\frac{2}{5}25  med 333, det vill säga 2⋅35⋅3=615\frac{2\cdot3}{5\cdot3}=\frac{6}{15}2·35·3 =615 

Du behöver inte göra en tabell som ovan, utan efter några försök är det enklare att använda multiplikationstabellen och på det viset lista ut vad bråktalen har för minsta gemensamma nämnare. Därför är det viktigt att du tränar dig på att känna igen olika multiplikationer.

Exempel

Exempel 1

Skriv bråktalen med minsta gemensamma nämnare

 36\frac{3}{6}36   och 23\frac{2}{3}23  

Lösning

Här är MGN: 6MGN:\text{ }6MGN: 6  eftersom att det är det minsta talet som finna i både 333 :ans och 666 :ans tabell.

Vi kan alltså förlänga 23=2⋅23⋅2=46\frac{2}{3}=\frac{2\cdot2}{3\cdot2}=\frac{4}{6}23 =2·23·2 =46  

 36\frac{3}{6}36   behöver vi inte förlänga då bråktalet redan står med nämnaren 666.

Exempel 2

Skriv bråktalen med minsta gemensamma nämnare

 78\frac{7}{8}78   och 23\frac{2}{3}23  

Lösning

Här är MGN: 24MGN:\text{ }24MGN: 24 eftersom att det är det minsta talet som finna i både 333 :ans och 888:ans tabell.

Vi förlänger då 23\frac{2}{3}23  med 888 så här

 23=2⋅83⋅8=1624\frac{2}{3}=\frac{2\cdot8}{3\cdot8}=\frac{16}{24}23 =2·83·8 =1624  

och  78\frac{7}{8}78  med 333 så här

 78=7⋅38⋅3=2124\frac{7}{8}=\frac{7\cdot3}{8\cdot3}=\frac{21}{24}78 =7·38·3 =2124  

Hitta minsta gemensam nämnare med primtalsfaktorisering

Det finns också en metod för att hitta MGN där primtalsfaktorisering används. När tal faktoriseras i primtal så delar du upp talen i faktorer som är primtal så långt det går. Vi skriver talet 121212 med primtalsfaktorer på följande vis.

 12=2⋅2⋅312=2\cdot2\cdot312=2·2·3

Här är faktorerna 2, 2, och 3 alla primtal. När de multipliceras med varandra får vi talet 121212. Det kan vara bra att kunna dela upp ett tal i primtalsfaktorer. Dessutom kan vi använda det till en metod för att hitta den gemensamma nämnaren.

Metod – MGN

  1. Dela upp nämnarna i primtalsfaktorer.
  2. Ta bort de gemensamma faktorerna.
  3. Multiplicera nämnarna med de övriga nämnarnas kvarstående faktorer.

I början kan det här verka ganska svårt. Men vi tar ett konkret exempel och hoppas det ska hjälpa.

Exempel 3

Använd metoden ovan och bestäm MGN för 16\frac{1}{6}16  och18\frac{1}{8}18 .

Lösning

1) Vi primtalsfaktoriserar de bägge nämnarna.

 6=2⋅36=2\cdot36=2·3 
 8=2⋅2⋅28=2\cdot2\cdot28=2·2·2 

2) De bägge talen har den gemensamma faktorn 222. Vi ”tar bort” den faktorn.

3) Vi multiplicerar därför 8⋅3=248\cdot3=248·3=24 och 6⋅2⋅2=246\cdot2\cdot2=246·2·2=24 

Den minsta gemensamma nämnaren är därför 24.

Det är bra att även ta ett lite svårare exempel på den här metoden.

Exempel 4

Använd metoden ovan och bestäm MGN för 1438\frac{14}{38}1438   och 718\frac{7}{18}718  .

Lösning

1) Vi primtalsfaktoriserar de bägge nämnarna.

 38=2⋅1938=2\cdot1938=2·19 
 18=2⋅3⋅318=2\cdot3\cdot318=2·3·3 

2) De bägge talen har den gemensamma faktorn 222. Vi ”tar bort” den faktorn.

3) Vi multiplicerar därför 18⋅19=34218\cdot19=34218·19=342  och 38⋅3⋅3=34238\cdot3\cdot3=34238·3·3=342 

Den minsta gemensamma nämnaren är därför 342342342.

Nästa lektion: Jämföra bråk

Eddler
VÅR TJÄNST
POPULÄRA KURSER
FÖRETAGSINFO

  • Eddler AB
    Org.nr: 559029-8195
    Kungsladugårdsgatan 86
    414 76 Göteborg

    info@eddler.se
© 2024 EDDLER AB
  • Säker SSL-server